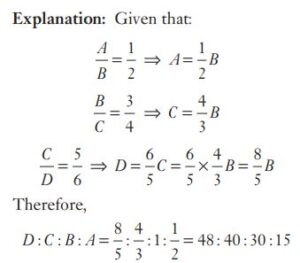Algebra Questions for SSC CGL

Algebra Questions for SSC CGL, CHSL, CPO with answers and solutions. Maths MCQs Mock Test for online practice of Competitive Exams.

Quiz : Algebra
Subject : Mathematics
Solved Objective Questions from the previous year papers

Results

Share your score!

Tweet your score!

#1. If $\frac{2p}{p^2 -2p + 1}$ = $\frac14$ , the value of $(p+\frac1p$ )is

7

\(\frac25\)

1

10

#2. If $\frac{2p}{p^2 -2p + 1}$ = $\frac14$ , the value of $(p+\frac1p$ )is

7

\(\frac25\)

1

10

#3. If a, b, c are real numbers and $a^2 + b^2 + c^ 2$ = 2 (a − b − c) − 3, then the value of a + b + c is

-1

1

3

0

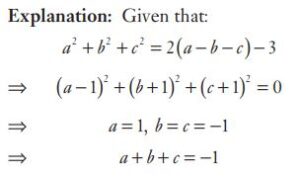
#4. If a = $\frac{\sqrt{x +2} +\sqrt{x-2}}{\sqrt{x +2} -\sqrt{x-2}}$ , then the value of $({a}^2 – ax$ ) is

1

2

-1

0

#5. If a = $\frac{\sqrt{x +2} +\sqrt{x-2}}{\sqrt{x +2} -\sqrt{x-2}}$ , then the value of $({a}^2 – ax$ ) is

1

2

-1

0

#6. If $a^2 + b^2 + c^2$ = ab + bc + ca, then the value of $\frac{a+ c }{b}$ is

3

2

0

1

#7. If $a^2 + b^2 + c^2$ = ab + bc + ca, then the value of $\frac{a+ c }{b}$ is

3

2

0

1

#8. $9x^2 + 25 − 30x$ can be expressed as the square of

−3x − 5

3x + 5

3x − 5

\(3x^2 − 25\)

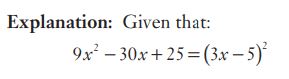
#9. If $\frac{a}{b} +\frac {b}{a} = 2$ , then the value of (a – b) is

1

-1

2

0

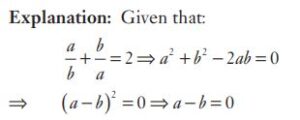
#10. If $\frac{a}{b} +\frac {b}{a} = 2$ , then the value of (a – b) is

1

-1

2

0

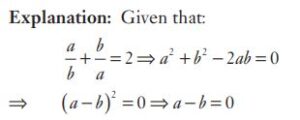
#11. If $\sqrt {y} = 4x$ , then $\frac{x^2}{y}$ is

2

\(\frac{1}{16}\)

\(\frac14\)

4

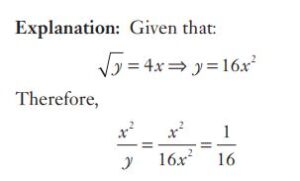
#12. If $\sqrt {y} = 4x$ , then $\frac{x^2}{y}$ is

2

\(\frac{1}{16}\)

\(\frac14\)

4

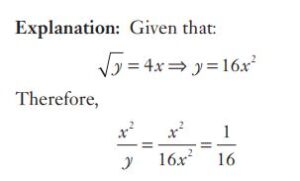
#13. If a + b = 1, c + d = 1 and a – b = $\frac{d}{c}$ , then the value of ${c^2} -{d^2}$ is :

\(\frac{a}{b}\)

\(\frac{b}{a}\)

1

-1

#14. If a + b = 1, c + d = 1 and a – b = $\frac{d}{c}$ , then the value of ${c^2} -{d^2}$ is :

\(\frac{a}{b}\)

\(\frac{b}{a}\)

1

-1

#15. If $(x − 2)$ is a factor of $x^2 + 3Qx − 2Q$ , then the value of Q is :

2

-2

1

-1

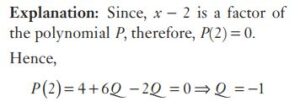
#16. If $a^2 + b^2 = 5ab$ , then the value of $(\frac{a^2}{b^2} +\frac{b^2}{a^2})$ is

32

16

23

-23

#17. If $a^2 + b^2 = 5ab$ , then the value of $(\frac{a^2}{b^2} +\frac{b^2}{a^2})$ is

32

16

23

-23

#18. If $a^2 − 4a − 1 = 0$ , then the value of $a^2 +\frac{1}{a^2} + 3a – \frac{3}{a}$ is

25

30

35

40

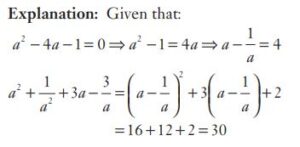
#19. If $a^2 − 4a − 1 = 0$ , then the value of $a^2 +\frac{1}{a^2} + 3a – \frac{3}{a}$ is

25

30

35

40

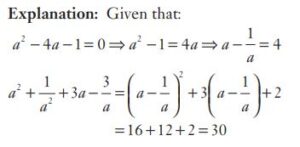
#20. If $x^2 − y^2 = 80$ and $x − y = 8$ , then the average of $x$ and $y$ is

2

4

3

5

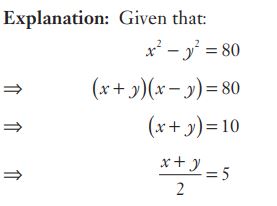
#21. If $x – \frac{1}{x} = 5$ , then $x^2 + \frac{1}{x^2}$ is

5

25

27

23

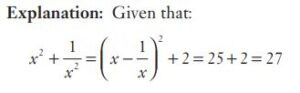
#22. If $x – \frac{1}{x} = 5$ , then $x^2 + \frac{1}{x^2}$ is

5

25

27

23

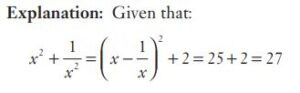
#23. If $x^2 + y^2 − 4x − 4y + 8 = 0$ , then the value of $x − y$ is

4

-4

0

8

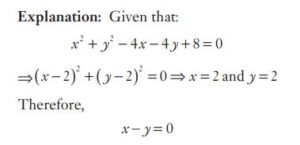
#24. If $x^2+ y^2 +2x + 1 = 0$ , then the value of $x^{31} + y^{35}$ is

-1

0

1

2

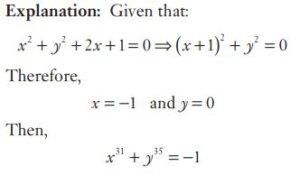
#25. If $x − y = 2$ and $x^2 + y^2 = 20$ , then the value of $(x + y) ^2$ is

38

36

16

12

#26. If $n +\frac{2}{3}n +\frac {1}{2}n +\frac{1}{7}n = 97$ , then the value of n is :

40

42

44

46

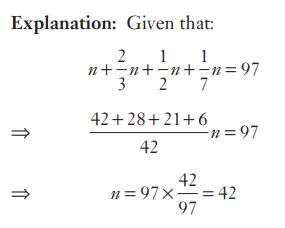
#27. If $n +\frac{2}{3}n +\frac {1}{2}n +\frac{1}{7}n = 97$ , then the value of n is :

40

42

44

46

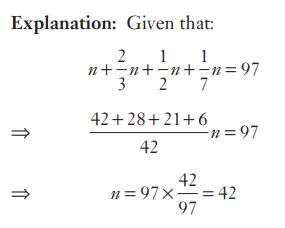
#28. If ${x^x}^\sqrt x$ = $(x\sqrt{x})^x$ , then $x$ equals

\(\frac49\)

\(\frac23\)

\(\frac94\)

\(\frac32\)

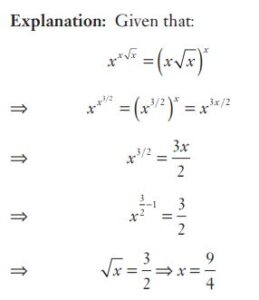
#29. If ${x^x}^\sqrt x$ = $(x\sqrt{x})^x$ , then $x$ equals

\(\frac49\)

\(\frac23\)

\(\frac94\)

\(\frac32\)

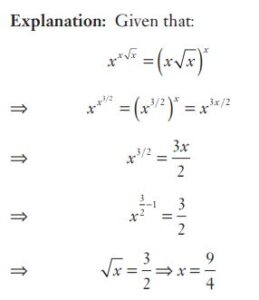
#30. If $p^3 – q^3 = ( p – q) {\{(p + q)^2 – xpq}\}$ , then the value of $x$ is

1

-1

2

-2

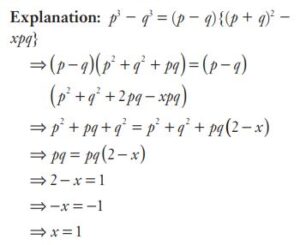
#31. If $p^3 – q^3 = ( p – q) {\{(p + q)^2 – xpq}\}$ , then the value of $x$ is

1

-1

2

-2

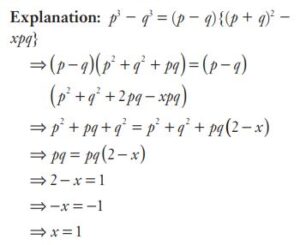
#32. If $x + y + z = 6$ , then the value of $(x − 1)^3 + (y − 2)^3 + (z − 3)^3$ is

\(3 (x − 1) (y − 2) (z − 3)\)

\(3xyz\)

\((x − l) (y − 2) (z − 3)\)

\(2(x − l) (y − 2) (z − 3)\)

#33. If $x^2 + y^2 + z^2 = 2 (x + z − 1)$ , then the value of $x^3 + y^3 + z^3$ is

2

0

-1

1

#34. If $x + y + z = 6$ and $xy + yz + zx = 10$ , then the value of $x^3 + y^3 + z^3 − 3xyz$ is

36

48

42

40

#35. The simplified value of the following is : $(\frac{3}{15} a^5 b^6 c^3 \times \frac{5}{9} ab^5 c^4)$ $\div\frac {10}{27} a^2 bc^3$

\(\frac{9a^2bc^4}{10}\)

\(\frac{3ab^4c^3}{10}\)

\(\frac{3a^4b^10c^4}{10}\)

\(\frac{1a^4b^4c^{10}}{10}\)

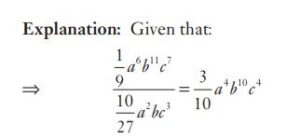
#36. The simplified value of the following is : $(\frac{3}{15} a^5 b^6 c^3 \times \frac{5}{9} ab^5 c^4)$ $\div\frac {10}{27} a^2 bc^3$

\(\frac{9a^2bc^4}{10}\)

\(\frac{3ab^4c^3}{10}\)

\(\frac{3a^4b^10c^4}{10}\)

\(\frac{1a^4b^4c^{10}}{10}\)

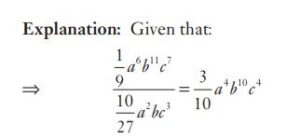
#37. If $x = 6 + \frac{1}{x}$ , then the value of $x^4 +\frac{1}{x^4}$ is

1448

1442

1444

1446

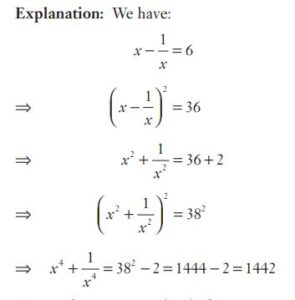
#38. If $x = 6 + \frac{1}{x}$ , then the value of $x^4 +\frac{1}{x^4}$ is

1448

1442

1444

1446

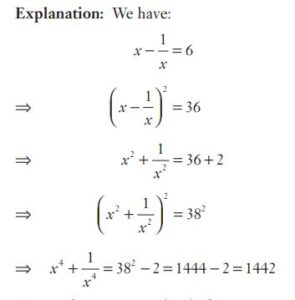
#39. If $x (x − 3) = − 1$ , then the value of $x^3 (x^3 − 18)$ is

-1

2

1

0

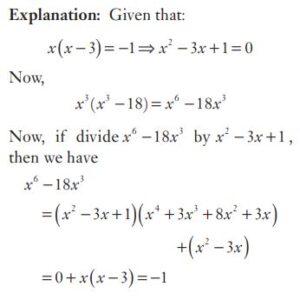
#40. If $x + \frac{1}{x} = 3$ , then the value of $\frac{3x^2 + 4x + 3}{x^2 – x + 1}$ is

\(\frac43\)

\(\frac32\)

\(\frac52\)

\(\frac53\)

#41. If $x + \frac{1}{x} = 3$ , then the value of $\frac{3x^2 + 4x + 3}{x^2 – x + 1}$ is

\(\frac43\)

\(\frac32\)

\(\frac52\)

\(\frac53\)

#42. If $x^3 + y^3 = 35$ and $x + y = 5$ , then the value of $\frac {1}{x} +\frac{1}{y}$ will be

\(\frac{1}{3}\)

\(\frac{5}{6}\)

6

\(\frac{2}{3}\)

#43. If $x^3 + y^3 = 35$ and $x + y = 5$ , then the value of $\frac {1}{x} +\frac{1}{y}$ will be

\(\frac{1}{3}\)

\(\frac{5}{6}\)

6

\(\frac{2}{3}\)

#44. If $x = a (b − c), y = b(c − a)$ and $z = c (a – b)$ , then $(\frac{x}{a})^3 +(\frac{y}{b})^3 +(\frac{z}{c})^3$ =

\(\frac{xyz}{3abc}\)

\(3 xyzabc\)

\(\frac{3xyz}{abc}\)

\(\frac{xyz}{abc}\)

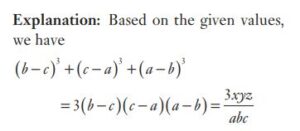
#45. If $x = a (b − c), y = b(c − a)$ and $z = c (a – b)$ , then $(\frac{x}{a})^3 +(\frac{y}{b})^3 +(\frac{z}{c})^3$ =

\(\frac{xyz}{3abc}\)

\(3 xyzabc\)

\(\frac{3xyz}{abc}\)

\(\frac{xyz}{abc}\)

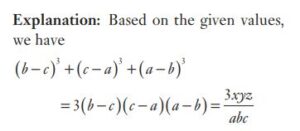
#46. If a/b = 1/2, then find the value of the expression (2a − 5b)/(5a + 3b)

-\(\frac85\)

-\(\frac{8}{11}\)

-\(\frac65\)

-\(\frac54\)

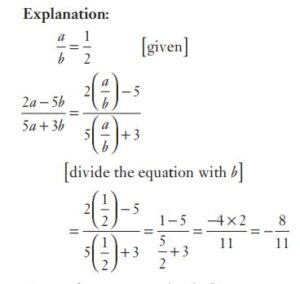
#47. If $x^2 + 9y^2 = 6xy$ , then $x : y$ is

1 : 3

3 : 2

3 : 1

2 : 3

#48. If A : B = 1 : 2, B : C = 3 : 4 and C : D = 5 : 6, find D : C : B : A

6 : 5 : 4 : 2

6 : 3 : 2 : 1

6 : 4 : 2 : 1

48 : 40 : 30 : 15

Previous

FINISH