RPF SI Mock Test in Hindi 1

(\(1 - 2x)^2\) - (\(1+2x)^2\)

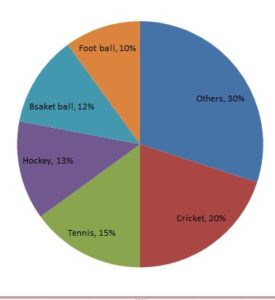
Cricket = क्रिकेट Tennis = टेनिस Foot ball =  फ़ुटबाॅल Basket ball =  बास्केटबाॅल Hockey = हाॅकी  Others = अन्य 

प्रश्न :  यदि वर्ष  के दौरान खेलों पर व्यय की गई कुल राशि रु 75,00,000 थी, तो क्रिकेट और हाॅकी पर कुल मिलाकर कितनी राशि (रु में ) व्यय की गई थी ?

अधिकतम कमाई वाले क्षेत्र और न्यूनतम कमाई वाले क्षेत्र से होने वाली आय के बीच अंतर (लाख में ) कितना हैं ?

42, 53, 46, ?, 53, 66

94 C 12 B 6 A 216 D 9 = ?

45 - 3 \(\div\) 144 \(\times\) 12 + 38 = ?

कथन :
I.सभी चाय, काॅफी हैं ?
II. सभी काॅफी, पेय पदार्थ हैं |
III. कुछ चाय , ड्रिंक हैं |
निष्कर्ष : 
I. सभी चाय, पेय पदार्थ हैं |
II. कोई ड्रिंक , काॅफी नहीं हैं |

ZFKQ, BCMN, ?, FWQH, HTSE

32 : 10 : : 24 : 12 : : 98 : ?

1. Desperate
2. Desolate
3. Destruction
4. Desire
5. Descend
6. Destination

परम के दाई ओर स्थान पर कौन बैठा हैं ?

729\(\times\) 9 - (56 - 6) \(\times\) 5\(\div\) 2 + 152 \(\times\) 19 = 69

(नोट : संख्यांओं को उस घटक अंकों में विभाजित किए बिना, पूर्ण संख्यांओं पर संक्रियाएँ की जानी चाहिए | उदाहरण के लिए  13 - इसमें 13 पर जोड़ने /घटाने /गुणा करने आदि जैसी संक्रियाओं  को 13 मे किया जा सकता हैं | 13 को 1 और 3 में विभाजित करने और फिर 1 और 3 पर गणितीय संक्रियाऍ करने की अनुमति नहीं हैं )
(7, 52), (9, 84)

32, 32, 32, 34, ?, 106, 530

1. Flint
2. Flec
3. Flaw
4. Fleet
5. Flight

(नोट : संख्यांओं को उसके घटक अंकों में विभाजित किए बिना, पूर्ण संख्यांओं पर गणितीय संक्रियाएँ की जानी चाहिए | उदाहरण के लिए  13  13 गणितीय संक्रियाएँ जैसे की जोड़ना /घटाना /गुणा करना  इत्यादि  13 मे किया जा सकता हैं | 13 को 1 और 3 में विभाजित करने और फिर 1 और 3 पर गणितीय संक्रियाऍ करने की अनुमति नहीं हैं )
(23 , 6, 35)
(13, 5, 23)

कथन :
कुछ खजूर हेजलनट  हैं|
सभी हेजलनट अखरोट हैं |
निष्कर्ष : 
I. कुछ खजूर अखरोट हैं |
II. कुछ अखरोट हेजलनट हैं |

HKOE, KNOE, ?, QTOE, TWOE

_ L _ _ K S _ T U_ S L _ _ K

8 \(\div\) 5 - 5 \(\times\) 10 + 2 = ?