Trigonometry Questions with Solution for SSC CGL, CHSL, CPO Competitive Exams. Mock Test for free online practice – All type from previous year papers.
Quiz : Trigonometry MCQs
Subject : Mathematics
Important Questions with Solutions
Results
#1. If \(0 \leq\theta\leq\frac{\pi}{2}\) and \(sec^2\theta + tan^2\theta = 7 \) then \(\theta\) is

#2. If \(0 \leq\theta\leq\frac{\pi}{2}\) and \(sec^2\theta + tan^2\theta = 7 \) then \(\theta\) is

#3. If the sum and difference of two angles are \(\frac{22}{9}\) radian and 36° respectively, then the value of smaller angle in degree taking the value of \(\pi\) as \(\frac{22}{7}\) is.

#4. If the sum and difference of two angles are \(\frac{22}{9}\) radian and 36° respectively, then the value of smaller angle in degree taking the value of \(\pi\) as \(\frac{22}{7}\) is.

#5. In circular measure, the value of the angle \(11^\circ\)15′ is
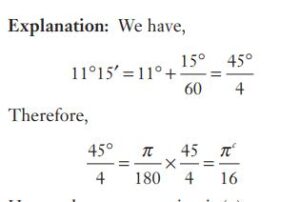
#6. In circular measure, the value of the angle \(11^\circ\)15′ is
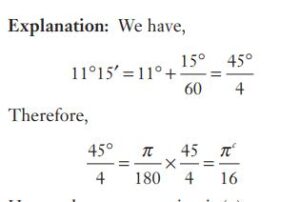
#7. Solve cot \( 9^\circ\) cot \(27^\circ\) cot \(63^\circ\) cot \(81^\circ\)

#8. Solve cot \( 9^\circ\) cot \(27^\circ\) cot \(63^\circ\) cot \(81^\circ\)

#9. If tan θ − tan 30° tan 60° and θ is an acute angle, then 2θ is equal to

#10. If \(tan\:θ + cot\:θ = 5\), then \(\tan^2\:θ + cot^2\:θ\) is
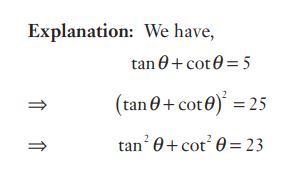
#11. If \(tan\:θ + cot\:θ = 5\), then \(\tan^2\:θ + cot^2\:θ\) is
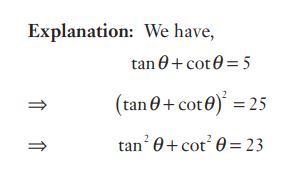
#12. If \(\frac{x - x\:tan^2 30^\circ}{1 + tan^2 30^\circ} = sin^2 30^\circ + 4\:cot^2 45 ^\circ - sec^2 60^\circ\), then the value of \(x\) is
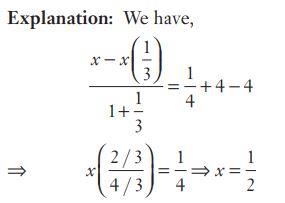
#13. If \(\frac{x - x\:tan^2 30^\circ}{1 + tan^2 30^\circ} = sin^2 30^\circ + 4\:cot^2 45 ^\circ - sec^2 60^\circ\), then the value of \(x\) is
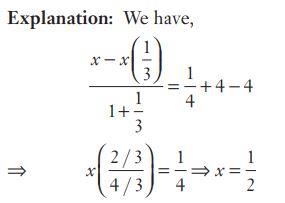
#14. If \(\frac{ sin\theta + cos\theta}{sin\theta - cos\theta} = 3\), then the value of \(sin^4 \theta\) is
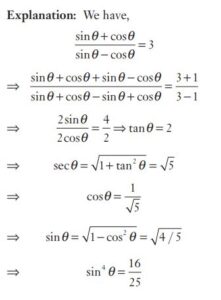
#15. If \(\frac{ sin\theta + cos\theta}{sin\theta - cos\theta} = 3\), then the value of \(sin^4 \theta\) is
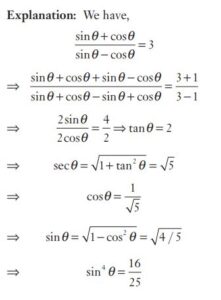
#16. If \(sin A + sin^2 A = 1\), then the value of \(cos^2 A + cos^4 A\) is
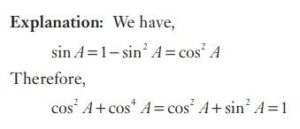
#17. If \(4sin^2 \theta - 1 = 0\) and the angle \(\theta\) is less than 90°, then the value of \(cos^2 \theta + \tan^2 \theta \) \((take\: 0^\circ <\theta< 90^\circ)\) is

#18. If \(4sin^2 \theta - 1 = 0\) and the angle \(\theta\) is less than 90°, then the value of \(cos^2 \theta + \tan^2 \theta \) \((take\: 0^\circ <\theta< 90^\circ)\) is

#19. If \(sec\:x + cos\:x = 2\), then the value of \(sec^{16}\:x + cos^{16} \:x\) will be.
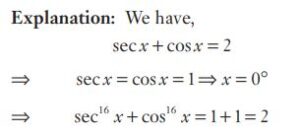
#20. If \(sec\:x + cos\:x = 2\), then the value of \(sec^{16}\:x + cos^{16} \:x\) will be.
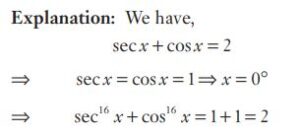
#21. If \(cos\:x + cos^2\:x = 1\), then \(sin^8\: x + 2 sin^6 \:x + sin^4\:x\) is equal to
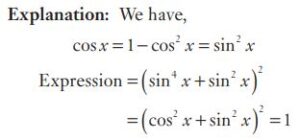
#22. If \(cos\:x + cos^2\:x = 1\), then \(sin^8\: x + 2 sin^6 \:x + sin^4\:x\) is equal to
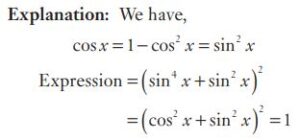
#23. If A is an acute angle and cot A + cosec A = 3, then the value of sin A is :
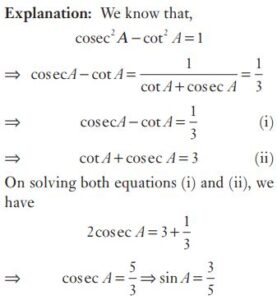
#24. If tan \(9^\circ = \frac {p}{q}\), then the value of \(\frac{sec^2\: 81^\circ}{1 + cot^2\: 81^\circ}\) is

#25. If tan \(9^\circ = \frac {p}{q}\), then the value of \(\frac{sec^2\: 81^\circ}{1 + cot^2\: 81^\circ}\) is

#26. If \(\sin θ =\frac {3}{5}\) , then the value of \(\frac {tan\:\theta + cos\: \theta}{cot\:\theta + cosec\: \theta}\) is equal to
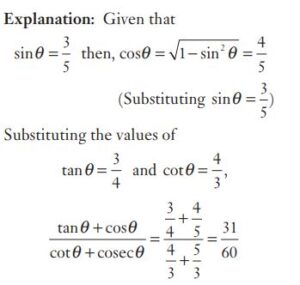
#27. If \(\sin θ =\frac {3}{5}\) , then the value of \(\frac {tan\:\theta + cos\: \theta}{cot\:\theta + cosec\: \theta}\) is equal to
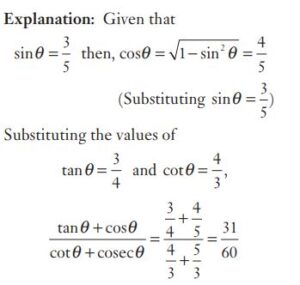
#28. If α and β are positive acute angles, then sin (4α - β) = 1 and cos (2α + β) = \(\frac12\), then the value of sin (α + 2β) is
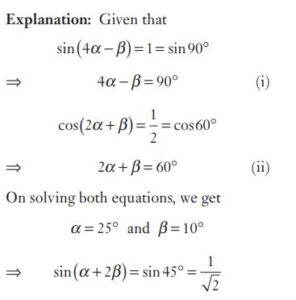
#29. If α and β are positive acute angles, then sin (4α - β) = 1 and cos (2α + β) = \(\frac12\), then the value of sin (α + 2β) is
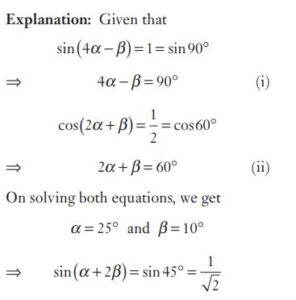
#30. Simplify: \(\frac{sin\:25^\circ cos\: 65^\circ + cos \:25^\circ sin \:65^\circ}{tan^2\: 70^\circ - cosec^2 \:20^\circ}\)

#31. Simplify: \(\frac{sin\:25^\circ cos\: 65^\circ + cos \:25^\circ sin \:65^\circ}{tan^2\: 70^\circ - cosec^2 \:20^\circ}\)

#32. If \(0° < 0 < 90°\) and \(2 sin^2\: θ + 3 cos\:θ = 3\), then the value of θ is
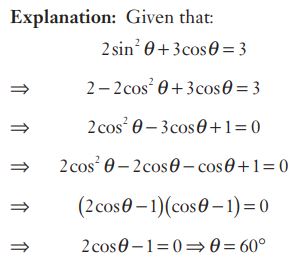
#33. If \(0° < 0 < 90°\) and \(2 sin^2\: θ + 3 cos\:θ = 3\), then the value of θ is
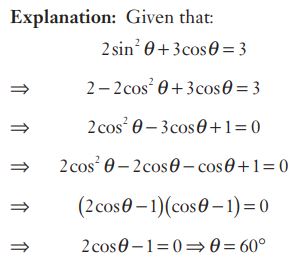
#34. If \(tan θ +cot θ = 2\) , then the value of \( tan^{100}\: \theta + cot^{100} \theta\) is
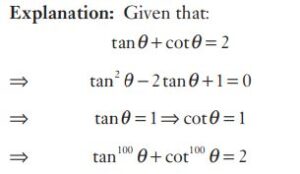
#35. If \(tan θ +cot θ = 2\) , then the value of \( tan^{100}\: \theta + cot^{100} \theta\) is
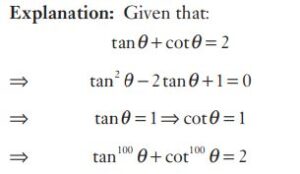
#36. The equation \(cos^2 \: \theta = \frac {(x+y)^2}{4xy}\) is only possible when

#37. The equation \(cos^2 \: \theta = \frac {(x+y)^2}{4xy}\) is only possible when

#38. If \(cos ^4\: \theta - sin^ 4\: \theta = \frac {2}{3}\), then the value of 1 - 2 \(sin^2\:\theta\) is
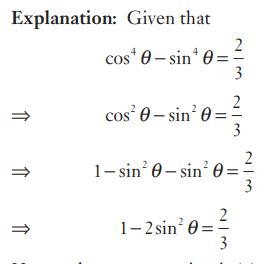
#39. If \(cos ^4\: \theta - sin^ 4\: \theta = \frac {2}{3}\), then the value of 1 - 2 \(sin^2\:\theta\) is
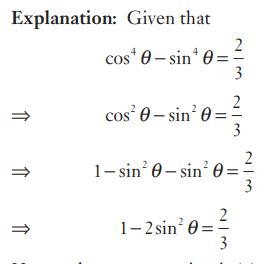
#40. If \( 7 sin^2\: \theta + 3 \:cos^2\: \theta = 4 (0° \leq \: \theta\: \leq 90^\circ)\), then the value of θ is :
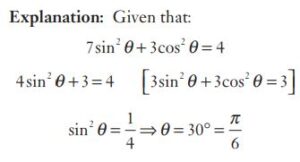
#41. If \( 7 sin^2\: \theta + 3 \:cos^2\: \theta = 4 (0° \leq \: \theta\: \leq 90^\circ)\), then the value of θ is :
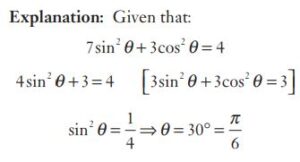
#42. If A = tan 11° tan 29°, B = 2 cot 61° cot 79°, then which of the following is correct?

#43. The measure of the angles of a triangle is in the ratio 2 : 7 : 11. The measures of angle are
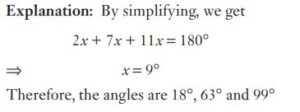
#44. A 10 metre long ladder is placed against a wall. It is inclined at an angle of 30° to the ground. The distance (in m) of the foot of the ladder from the wall is (Given = \(\sqrt3 =1.732)\)
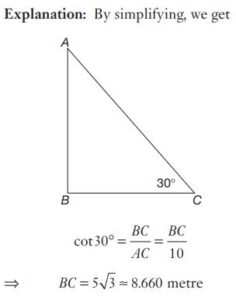
#45. A 10 metre long ladder is placed against a wall. It is inclined at an angle of 30° to the ground. The distance (in m) of the foot of the ladder from the wall is (Given = \(\sqrt3 =1.732)\)

#46. If a 48 m tall building has a shadow of 48 \(\sqrt3\) m, then the angle of elevation of the sun is

#47. If a 48 m tall building has a shadow of 48 \(\sqrt3\) m, then the angle of elevation of the sun is

#48. The angle of elevation of sun changes from 30° to 45°, the length of the shadow of a pole decreases by 4 metres, the height of the pole is (Assume \(\sqrt3 =1.732\))

#49. The angle of elevation of sun changes from 30° to 45°, the length of the shadow of a pole decreases by 4 metres, the height of the pole is (Assume \(\sqrt3 =1.732\))

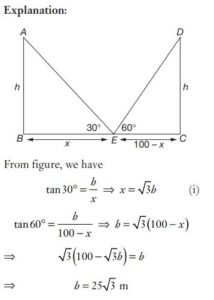
#50. Two poles of equal height are standing opposite to each other on either side of a road which is 100 m wide. From a point between them on road, the angles of elevation of their tops are 30° and 60° The height of each pole (in metre) is
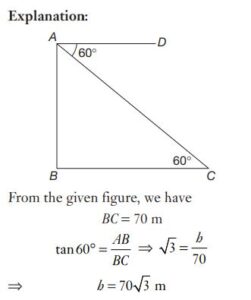
#51. The angle of depression of a point situated at a distance of 70 m from the base of a tower is 60° The height of the tower is :
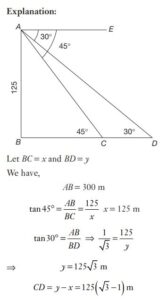
#52. From a tower 125 metres high, the angle of depression of two objects, which are in horizontal line through the base of the tower are 45° and 30° and they are on the same side of the tower. The distance (in metres) between the objects is