Geometry Objective Questions with Solution for SSC CGL, CHSL Competitive Exams. All type MCQs Mock Test for online practice.
Quiz : Geometry
Subject : Mathematics
Medium : English
Important questions with answer from previous year SSC papers
Solution with Short tricks
Press Finish / Submit button for the result and see the solution of all Geometry questions.
Results
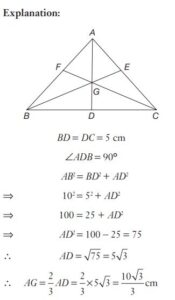
#1. The centroid of an equilateral triangle ABC is G and AB is 10 cm. The length of AG (in cm) is
#2. The side BC of a triangle ABC is extended to D. If \(\angle ACD = 120°\) and \(\angle ABC = \frac{1}{2} \angle CAB\), then the value of \(\angle ABC\) is
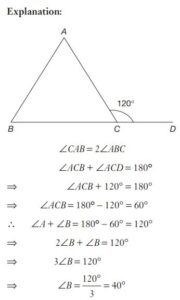
#3. The side BC of a triangle ABC is extended to D. If \(\angle ACD = 120°\) and \(\angle ABC = \frac{1}{2} \angle CAB\), then the value of \(\angle ABC\) is

#4. In a triangle, if three altitudes are equal, then the triangle is :
Explanation: Triangle will be equilateral.
Hence, the correct option is
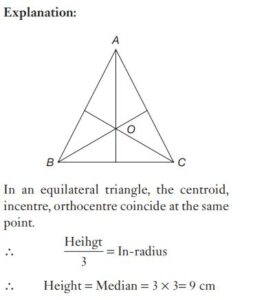
#5. The in-radius of an equilateral triangle is of length 3 cm. Then the length of each of its medians is
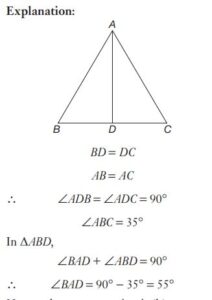
#6. ABC is an isosceles triangle such that AB = AC and AD is the median to the base BC with ∠ABC = 35°. Then ∠BAD is
#7. If angle bisector of a triangle bisects the opposite side, then what type of triangle is it?

#8. In a triangle \(ABC, AB = AC, \angle BAC = 40^\circ\) Then the external angle at B is :
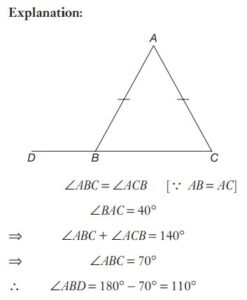
#9. In a triangle \(ABC, AB = AC, \angle BAC = 40^\circ\) Then the external angle at B is :

#10. ABC is a triangle and the sides AB, BC and CA are produced to E, F and G respectively. If \(\angle CBE = \angle ACF = 130^\circ \) then the value of \(\angle GAB\) is
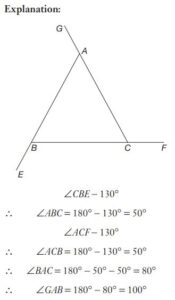
#11. ABC is a triangle and the sides AB, BC and CA are produced to E, F and G respectively. If \(\angle CBE = \angle ACF = 130^\circ \) then the value of \(\angle GAB\) is

#12. In \(∆ABC \angle B = 60°, and \angle C = 40^\circ\), AD and AE are respectively the bisector of \(\angle A\) and perpendicular on BC. The measure of \(\angle EAD\) is
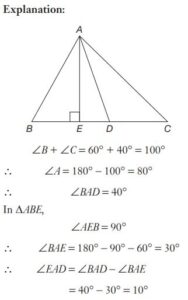
#13. In \(∆ABC \angle B = 60°, and \angle C = 40^\circ\), AD and AE are respectively the bisector of \(\angle A\) and perpendicular on BC. The measure of \(\angle EAD\) is

#14. The side BC of a triangle ABC is produced to D. If \(\angle ACD = 112^\circ\) and \(\angle B =\frac {3}{4} \angle A\), then the measure of \(\angle B\)

#15. The side BC of a triangle ABC is produced to D. If \(\angle ACD = 112^\circ\) and \(\angle B =\frac {3}{4} \angle A\), then the measure of \(\angle B\)

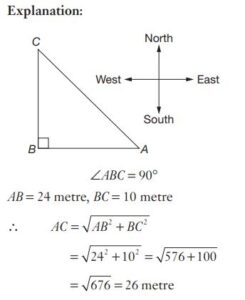
#16. A man goes 24 m due west and then 10 m due north. Then the distance of him from the starting point is
#17. In \(∆ABC, \angle B = 60°,\angle C = 40^\circ, AD\) is the bisector of \(\angle A\) and AE is drawn perpendicular on BC from A. Then the measure of \(\angle EAD\) is
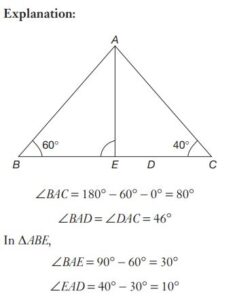
#18. In \(∆ABC, \angle B = 60°,\angle C = 40^\circ, AD\) is the bisector of \(\angle A\) and AE is drawn perpendicular on BC from A. Then the measure of \(\angle EAD\) is

#19. I is the incentre of \(∆ABC, \angle ABC = 60^\circ \) and \(\angle ACB = 50^\circ\). Then \(\angle BIC\) is
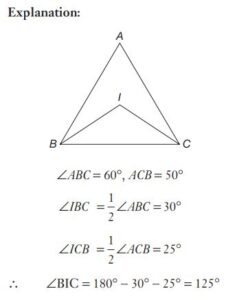
#20. I is the incentre of \(∆ABC, \angle ABC = 60^\circ \) and \(\angle ACB = 50^\circ\). Then \(\angle BIC\) is

#21. If the sides of a triangle are in the ratio \(3 : 1\frac{1}{4}: 3\frac{1}{4}\) then the triangle is .

#22. If the sides of a triangle are in the ratio \(3 : 1\frac{1}{4}: 3\frac{1}{4}\) then the triangle is .

#23. In ∆ABC, ∠B = 90°, AB = 8 cm and BC = 15 cm, then sin C = ?

#24. If the sides of a right angled triangle are three consecutive integers, then the length of the smallest side is

#25. In a ∆ABC, D and E are two points on AB and AC respectively such that DE || BC, DE bisects the ∆ABC in two equal areas. Then the ratio of DB : AB is

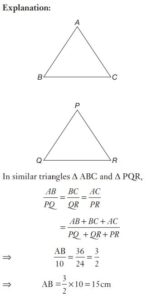
#26. The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then AB is
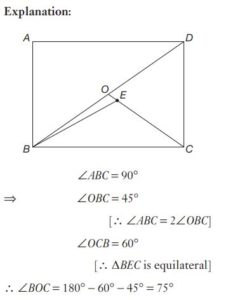
#27. Inside a square ABCD, ∆ BEC is an equilateral triangle. If CE and BD intersect at O, then ∠BOC is equal to
#28. The measure of each interior angle of a regular polygon with 8 sides is

#29. The sum of interior angles of a regular polygon is 1440° The number of sides of the polygon is

#30. The sum of all internal angles of a regular polygon whose one external angle is 20° is

#31. The number of sides in two regular polygons are in the ratio 5 : 4 and the difference between each interior angle of the polygons is 6°. Then the number of sides is :
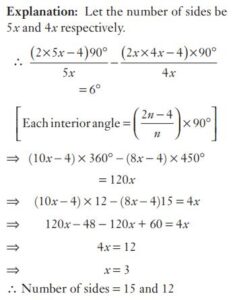
#32. The length of the diagonal BD of the parallelogram ABCD is 18 cm. If P and Q are the centroid of the ∆ABC and ∆ADC respectively then the length of the line segment PQ is :
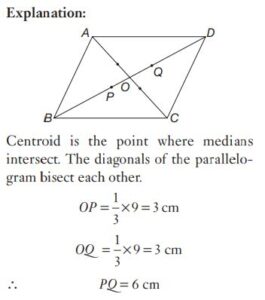
#33. The point of intersection of the diagonals AC and BD of the cyclic quadrilateral ABCD is P. If \(\angle APB = 64^\circ\) and \(\angle CBD = 28^\circ\). The measure of \(\angle ADB\) is
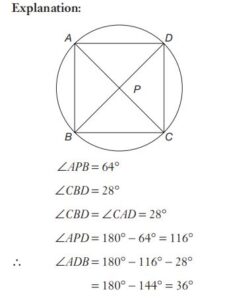
#34. The point of intersection of the diagonals AC and BD of the cyclic quadrilateral ABCD is P. If \(\angle APB = 64^\circ\) and \(\angle CBD = 28^\circ\). The measure of \(\angle ADB\) is

#35. AB is a diameter of a circle having centre at O. PQ is a chord which does not intersect AB. Join AP and BQ. If \(\angle BAP = \angle ABQ\), then ABQP is a
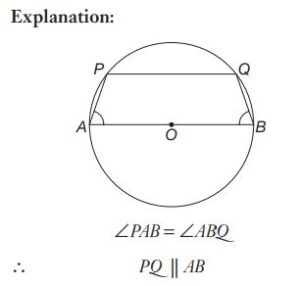
#36. AB is a diameter of a circle having centre at O. PQ is a chord which does not intersect AB. Join AP and BQ. If \(\angle BAP = \angle ABQ\), then ABQP is a

#37. Three circles of radius 6 cm each touch each other externally. Then the distance of the centre of one circle from the line joining the centres of other two circles is equal to
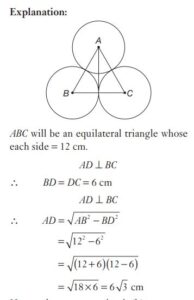
#38. Two circles having radii r units intersect each other in such a way that each of them passes through the centre of the other. Then the length of their common chord is
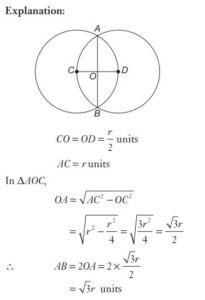
#39. The distance between two parallel chords of length 8 cm each in a circle of diameter 10 cm is

#40. Two circles with their centres at O and P and radii 8 cm and 4 cm respectively touch each other externally. The length of their common tangent is

#41. If AB = 5 cm, AC = 12 cm and AB ⊥ AC, then the radius of the circumcircle of ∆ABC is
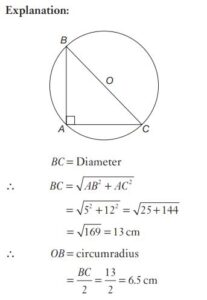
#42. The ratio of circumradius and radius of an equilateral triangle is

#43. A tree of hight ‘h’ metres is broken by a storm in such a way that it’s top touches the ground at a distance of ‘x’ metres from its root. Find the height at which the tree is broken. (Here \(h > x)\)

#44. A and B are centres of two circles of radii 11 cm and 6 cm respectively. PQ is a direct common tangent to the circles. If \(\overline {AB} \)= 13 cm, then the length of \(\overline {PQ} \)will be
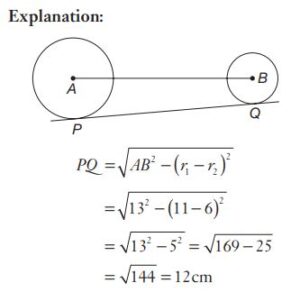
#45. A and B are centres of two circles of radii 11 cm and 6 cm respectively. PQ is a direct common tangent to the circles. If \(\overline {AB} \)= 13 cm, then the length of \(\overline {PQ} \)will be
