Quantitative Aptitude Questions with answers and Solutions for SSC CPO- SI in CPMF Exam. Maths MCQs Mock Test for free online practice of SI CAPF Exam.
Practice Set : Mathematics (Quantitative Aptitude)
Questions : 50
Medium : English
Level : SSC CPO SI Exam
All Type and topic MCQs – Solved by short tricks
Immediate display of Answer and Solution
New Practice of 50 Questions in every attempt
Results
#1. If the square of the sum of two numbers is equal to 4 times of their product, then the ratio of these numbers is :
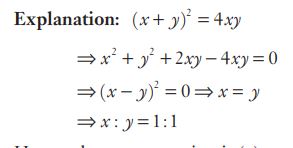
#2. To gain 8% after allowing a discount of 10%, by what percent cost price should be hiked in the list price?

#3. ![\sqrt[3]{(333)^3+(333)^3+(334)^3 -3\times333\times333\times334}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B%28333%29%5E3%2B%28333%29%5E3%2B%28334%29%5E3+-3%5Ctimes333%5Ctimes333%5Ctimes334%7D+&bg=ffffff&fg=000&s=0&c=20201002) is equal to
is equal to

#4. A box contains 280 coins of denomination carrying 1 rupee, 50 paise and 25 paise. The values of each kind of the coins are in the ratio of 8 : 4 : 3. Then the number of 50 paise coins is :

#5. One man or two women or three boys can do a piece of work in 88 days. One man, one women and one boy will do it in :
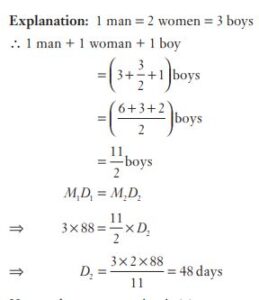
#6. A trader marked the price of a commodity so as to include a profit of 25%, but allowed a discount of 16% on the market price. His actual profit will be :

#7. The value of 

#8. The difference between the compound interest and simple interest on a certain sum for 2 years at 10% per annum is 300. Find the sum.
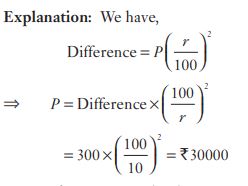
#9. The digit in unit’s place of the number (1570)2 + (1571)2 + (1572)2 + (1573)2 is :

#10. If 20% of A = 50% of B, then what per cent of A is B?

#11. Arvind purchased a wrist watch with 30% discount on the labelled price. He sold it with 40% profit on the price he bought. What was his per cent loss on the labelled price?

#12. The average of 30 numbers is 12. The average of the first 20 of them is 11 and that of the next 9 is 10. The last number is :
Explanation: Last number :
= 30 × 12-20 × 11 − 9 × 10
= 360 − 220 − 90
= 360 − 310 = 50
#13.  is equal to
is equal to

#14. A 200 metre long train is running at a speed of 72 km/hr. How long will it take to cross 800 metre long bridge?

#15. The marked price of a radio is Rs 4800. The shopkeeper allows a discount of 10% and gains 8%. If no discount is allowed, his gain per cent will be :

#16. . If x : y = 3 : 4, then 4x + 5y : 5x− 2y = ?
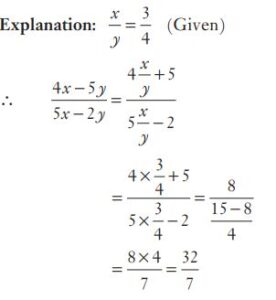
#17. Instead of multiplying a number by 0.72, a student multiplied it by 7.2. If his answer was 2592 more than the correct answer, then the original number was :

#18. On selling an article for Rs 105 a trader loses 9%. To gain 30% he should sell the article at

#19. Which of the following number is the greatest of all? 
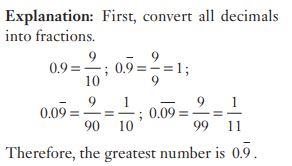
#20. A sum of money is divided among A, B, C and D in the proportion of 7 : 6 : 3 : 5. If B gets `270 more than C, then the share of D is :

#21. The average salary of all the workers in a workshop is Rs. 8000. The average salary of 7 technicians is Rs.12,000 and the average salary of the rest is Rs.6000. The total number of workers in the workshop is :

#22. If Rahim deposited the same amount of Rs x in a bank at the beginning of successive 3 years and the bank pays a simple interest of 5% per annum, then the amount at his credit at the end of 3rd year will be :

#23. If the ratio of principal and the simple interest for 5 years is 10 : 3, then the rate of interest is :
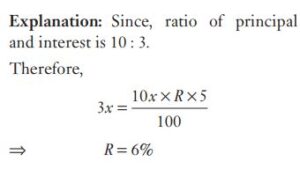
#24. By selling an article for Rs 69, there is a loss of 8%, when the article is sold for Rs 78, the gain or loss per cent is :

#25. The fourth proportional to 0.12, 0.21, 8 is :

#26. A supply of juice lasts for 35 days. If its use is increased by 40%, then the number of days would the same amount of juice lasts is :

#27. If in a sale, the discount given on a saree is equal to one-fourth the marked price and the loss due to this discount is 15%, then the ratio of the cost price to the selling price is :

#28. The least number, which is to be added to the greatest number of 4 digits so that the sum may be divisible by 345 is :

#29. What least number must be subtracted from 1936 so that the resulting number when divided by 9, 10 and 15 will leave in each case the same remainder 7 ?
LCM of 9, 10 and 15 = 90
The multiple of 90 are also divisible by 9, 10 or 15.
21 × 90 = 1890 will be divisible by them.
Now, 1897 will be the number
that will give remainder 7.
Required number = 1936 – 1897 = 39
#30. A and B can complete a piece of work in 8 days, B and C can do it in 12 days, C and A can do it in 8 days. A, B and C together can complete it in :
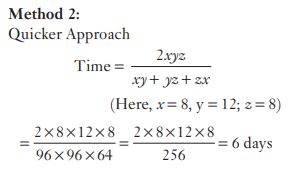
#31. Two numbers are in the ratio 1 : 3 If their sum is 240, then their difference is :

#32. The simplified value of  is
is
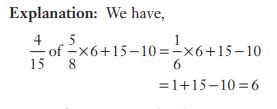
#33. A sum of Rs 1550 was lent partly at 5% and partly at 8% simple interest. The total interest received after 3 years is Rs 300. The ratio of money lent at 5% to that at 8% is :

#34. If the difference between S.I. and C.I. for 2 years on a sum of money lent at 5% is Rs 6, then the sum is :
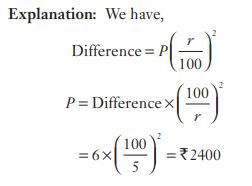
#35. A man with  of his usual speed reaches the destination
of his usual speed reaches the destination  hours late. Find his usual time to reach the destination .
hours late. Find his usual time to reach the destination .

#36. Every Sunday, Gin jogs 3 miles. For rest of the week, each day he jogs 1 mile more than the previous day. How many miles Gin jogs in 2 weeks?
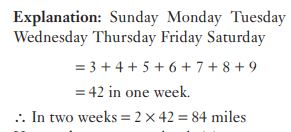
#37. A man bought a watch for 10% discount. If had bought for 20% discount he would have got the watch for Rs 125 less. The marked price of the watch is :

#38. By selling a tape-recorder for Rs 1040 a man gains 4%. If he sells for Rs 950, then his loss will be :

#39. A pipe can fill a tank in ‘x’ hours and another pipe can empty it in ‘y’ (y > x) hours. If both the pipes are open, in how many hours will the tank be filled?

#40. 16 men are able to complete a piece of work in 12 days working 14 hours a day. How long will 28 men, working 12 hours a day, take to complete the work?

#41. A student was asked to multiply a given number by  Instead, he divided the number by
Instead, he divided the number by  His answer was 225 more than the correct answer. The given number was :
His answer was 225 more than the correct answer. The given number was :
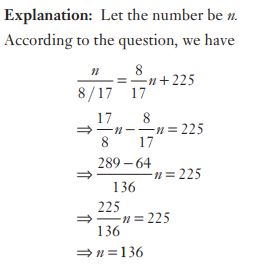
#42. A train passes two bridges of lengths 500 m and 250 m in 100 seconds and 60 seconds respectively. The length of the train is :

#43. What will come in place of the question mark (?) in the series? 3, 8, 27, 112, (?), 3396

#44. In a school 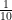 of the boys are same in number as
of the boys are same in number as  of the girls and
of the girls and  of the girls are same in number as
of the girls are same in number as  of the boys. The ratio of the boys to girls in that school is :
of the boys. The ratio of the boys to girls in that school is :
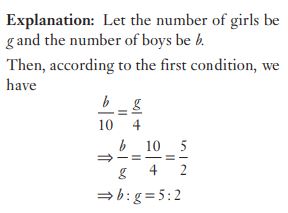
#45. The cost of manufacturing an article was Rs 900. The trader wants to gain 25% after giving a discount of 10%. The marked price must be :

#46. Which term of the series 72, 63, 54 … is zero?
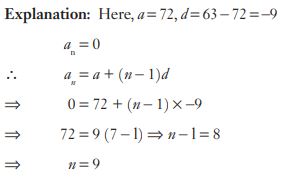
#47. Water tax is increased by 20% but its consumption is decreased by 20%. Then the increase or decrease in the expenditure of the money is :

#48. A boat goes 6 km an hour in still water, but takes thrice as much time in going the same distance against the current. The speed of the current (in km/hour) is :

#49. Find the selling price of an article if a shopkeeper allows two successive discounts of 5% each on the marked price of Rs 80

#50. 25% of annual salary of A is equal to eighty percent of annual salary of B. The monthly salary of B is 40% of the monthly salary of C. The annual salary of C is Rs. 6 lac. What is the monthly salary of A?
