LCM and HCF MCQ Questions Mock Test with answers and solution for Competitive Exams. Quantitative Aptitude (Math) – LCM HCF all type MCQs from previous year paper of SSC CGL, CHSL, Bank etc.
Practice Test : LCM and HCF Questions
Total Questions – 30
Type wise – Each type 5 MCQs
Medium : English
Feature :
Immediately show the correct Answer and Solution after selection of option
Full Result with answer – On Submit the Quiz.
Results
#1. Two numbers are in the ratio 3 : 4. Their LCM is 84. The greater number is

#2. Find the least multiple of 23, which when divided by 18, 21 and 24 leaves the remainder 7, 10 and 13 respectively.
LCM of 18, 21 and 24
LCM = 2 × 3 × 3 × 7 × 4 = 504
Now compare the divisors with their respective remainders. We observe that in all the cases the remainder is just 11 less than their respective divisor. So the number can be given by 504 K – 11 Where K is a positive integer
Since 23 × 21 = 483
We can write 504 K – 11
= (483 21) K – 11, = 483 K (21K – 11)
483 K is multiple of 23, since 483 is divisible by 23.
So, for (504K – 11) to be multiple of 23, the remainder (21K – 11) must be divisible by 23.
Put the value of K = 1, 2, 3, 4, 5,6, ….. and so on successively.
We find that the minimum value of K for which (21K – 11) is divisible by 23. is 6, (21 × 6 – 11)
= 115 which is divisible by 23.
Therefore, the required least number
= 504 × 6 – 11 = 3013
#3. The LCM of two numbers is 1920 and their HCF is 16. If one of the number is 128, find the other number.
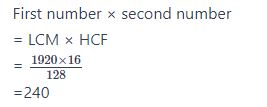
#4. LCM of 12 and 16 Prime factorisation of $latex 12 = 2^3 $ × 3 = 22 × 3 Prime factorisation of 16 = 2 × 2 × 2 × 2 = 24
[latex]e^{i pi} 1 = 0[/latex]
[latex]e^{i pi} 1 = 0[/latex]
[latex]e^{i pi} 1 = 0[/latex]
#5. The HCF and LCM of two numbers are 12 and 924 respectively. Then the number of such pairs is
Let the numbers be 12x and
12y where x and y are prime to
each other.
LCM = 12xy
12xy = 924
xy = 77
Possible pairs = (1,77) and (7,11)
#6. The HCF of two numbers is 96 and their LCM. is 1296. If one of the number is 864, the other is

#7. Product of two co-prime numbers is 117. Then their LCM is
HCF of two-prime numbers = 1
Product of numbers = their
LCM = 117
117 = 13 × 9 where 13 & 9 are
co-prime. L.C.M (13,9) = 117
#8. The HCF of two numbers is 8. Which one of the following can never be their LCM ?
HCF of two numbers is 8.This means 8 is a factor common to both the numbers. LCM is common multiple for the two numbers, it is divisible by the two numbers. So, the required answer = 60
#9. The least number which when divided by 4, 6, 8, 12 and 16 leaves a remainder of 2 in each case is :
L.C.M. of 4, 6, 8, 12 and 16 = 48
Required number = 48 2 = 50
#10. Find the largest number of four digits such that on dividing by 15,18, 21 and 24 the remainders are 11, 14, 17 and 20 respectively.

#11. The least perfect square, which is divisible by each of 21, 36 and 66 is

#12. What is the smallest number which leaves remainder 3 when divided by any of the numbers 5, 6 or 8 but leaves no remainder when it is divided by 9 ?

#13. What least number must be subtracted from 1936 so that the resulting number when divided by 9, 10 and 15 will leave in each case the same remainder 7 ?
LCM of 9, 10 and 15 = 90
The multiple of 90 are also divisible by 9, 10 or 15.
21 × 90 = 1890 will be divisible by them.
Now, 1897 will be the number
that will give remainder 7.
Required number = 1936 – 1897 = 39
#14. The greatest number, which when divide 989 and 1327 leave remainders 5 and 7 respectively, is :
The largest number which when divide the numbers a, b and c give remainders as p, q, r respectively is given by H.C.F. of (a – p), (b – q) and (c – r)
Required number
= HCF of (989 – 5) and (1327 – 7)
= HCF of 984 and 1320 = 24
HCF = 24
#15. HCF of \( \frac {2}{3} , \frac{4}{5} and \frac{6}{7} \) is
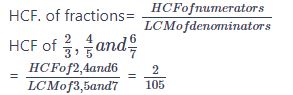
#16. The greatest number, by which 1657 and 2037 are divided to give remainders 6 and 5 respectively, is
The largest number which when divide the numbers a, b and c give remainders as p, q, r respectively is given by HCF of (a – p), (b – q) and (c – r)
Required number
We have to find HCF of
(1657 – 6 = 1651) and (2037 – 5 = 2032)
1651 = 13 × 127, 2032 = 16 × 127
HCF = 127 So, required number will be 127
#17. 84 Maths books, 90 Physics books and 120 Chemistry books have to be stacked topic wise. How many books will be there in each stack so that each stack will have the same height too ?
As the height of each stack is same, the required number of books in each stack
HCF of 84, 90 and 120
84 = 2 × 2 × 3 × 7, 90 = 2 × 3 × 3 × 5, 120 = 2 × 2 × 2 × 3 × 5
HCF = 2 × 3 = 6
#18. The product of two 2–digit numbers is 2160 and their HCF is 12. The numbers are

#19. If the ratio of two numbers is 2 : 3 and their LCM is 54, then the sum of the two numbers is
Let the two numbers are 2x and 3x respectively.
According to question,
LCM = 54
x (3×2)=54
x = 9
Numbers = 2x = 2 × 9 = 18 and 3x = 3 × 9 = 27
Sum of the two numbers
= 18 27 = 45
#20. Three numbers are in the ratio 2 : 3 : 4 and their HCF is 12. The L.C.M of the numbers is
Let the numbers be 2x, 3x and 4x respectively.
HCF = x = 12
Numbers are : 2 ×12 = 24
3 ×12 = 36, 4 ×12 = 48
LCM of 24, 36, 48
= 2 × 2 × 2 × 3 × 3 × 2 = 144
#21. Three numbers are in the ratio 1 : 2 : 3 and their HCF is 12. The numbers are
Numbers = x , 2 x and 3 x (let)
Their HCF = x = 12
Numbers = 12, 24 and 36
#22. The HCF and LCM of two numbers are 21 and 84 respectively. If the ratio the two numbers is 1 : 4, then the larger of the two numbers is
HCF of numbers = 21
Numbers = 21x and 21y
Where x and y are prime to each other.
Ratio of numbers = 1 : 4
Larger number = 21 × 4 = 84
#23. The sum of the HCF and LCM of two numbers is 680 and the LCM is 84 times the HCF If one of the number is 56, the other is :

#24. The sum of a pair of positive integer is 336 and their HCF is 21.The number of such possible pairs is
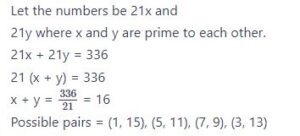
#25. The product of the LCM and the HCF of two numbers is 24. If the difference of the numbers is 2, then the greater of the number is
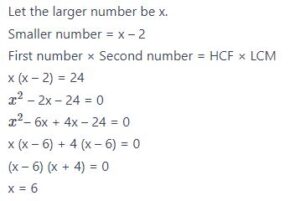
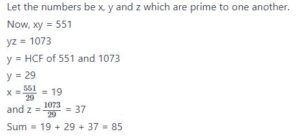
#26. Three numbers which are coprime to one another are such that the product of the first two is 551 and that of the last two is 1073. The sum of the three numbers is :
#27. If A and B are the HCF and LCM respectively of two algebraic expressions x and y, and A + B = x + y, then the value of \( A^3+B^3 \) is
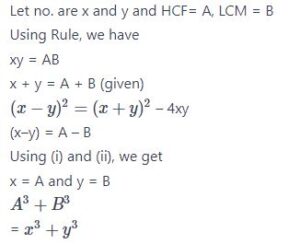
#28. The LCM of two multiples of 12 is 1056. If one of the number is 132, the other number is

#29. The least number to be subtracted from 36798 to get a number which is exactly divisible by 78 is
When 36798 is divided by 78, remainder = 60
The least number to be subtracted = 60
#30. The greatest number, that divides 122 and 243 leaving respectively 2 and 3 as remainders, is
Clearly, 122 – 2 = 120 and 243 – 3 = 240 are exactly divisible by the required number.
Required number
= HCF of 120 and 240 = 120
#31. The HCF (GCD) of a, b is 12, a, b are positive integers and a > b > 12. The smallest values of (a, b) are respectively
HCF of a and b = 12
Numbers = 12x and 12y where x and y are prime to each other.
a > b > 12
a = 36; b = 24



Mock test