SSC CPO Math Questions in Hindi – Mock Test of quantitative aptitude for SI CAPF Exam, Free online practice. Maths MCQs with answer and solution, from the previous year papers.
मॉक टेस्ट: गणित (मात्रात्मक योग्यता) प्रश्न
प्रश्नों की संख्या: 50 (प्रत्येक सेट में नए प्रश्न और प्रत्येक प्रयास में नया सेट)
स्तर: एसएससी सीपीओ सब इंस्पेक्टर परीक्षा
उत्तर और समाधान के साथ सभी प्रकार के प्रश्न
उत्तर और समाधान का तत्काल प्रदर्शन
नवीनतम परीक्षा पैटर्न और पाठ्यक्रम के अनुसार सभी अभ्यास सेट
Results
#1. एक संख्या को 221 से विभाजित करने पर शेषफल 64 बचता है। यदि उसी संख्या को 13 से विभाजित किया जाए तो शेषफल क्या होगा?

#2. एक फार्म में गायें और मुर्गियाँ हैं। यदि सिर गिने जाएँ तो 180 होंगे, यदि पैर गिने जाएँ तो 420 होंगे। फार्म में गायों की संख्या है:

#3. 800 रुपये अंकित मूल्य वाली एक वस्तु ऑफ सीजन में 736 रुपये में बेची जाती है। दी जाने वाली छूट की दर है |
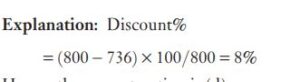
#4. 20% बढ़ी हुई संख्या के मान और 25% घटी हुई संख्या के मान के बीच का अंतर 36 है। संख्या ज्ञात कीजिए |

#5. एक लड़का और लड़की मिलकर एक टंकी को पानी से भरते हैं। लड़का हर 3 मिनट में 4 लीटर पानी डालता है और लड़की हर 4 मिनट में 3 लीटर पानी डालती है। टंकी में 100 लीटर पानी भरने में कितना समय लगेगा?

#6. वह छोटी से छोटी संख्या जिसे 36798 में से घटाने पर 78 से पूर्णतः विभाजित होने वाली संख्या प्राप्त हो
When 36798 is divided by 78, remainder = 60
The least number to be subtracted = 60
#7. दो संख्याओं के लघुतम समापवर्त्य और सबसे बड़े समापवर्तक का गुणनफल 24 है। यदि संख्याओं का अंतर 2 है, तो बड़ी संख्या है
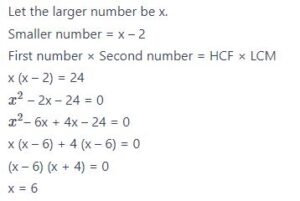
#8. यदि 2 + x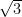 =
= तो x का सरलतम मान है :
तो x का सरलतम मान है :

#9. दो संख्याओं के बीच 5 : 4 का अनुपात है। यदि पहली संख्या का 40 प्रतिशत 12 है, तो दूसरी संख्या का 50% क्या है |

#10. अनुक्रम 169, 144, 121, 100, 82, 64, 49 में गलत संख्या ज्ञात कीजिए

#11. 16 साल पहले मेरे दादाजी मुझसे 9 गुना बड़े थे। आज से 8 साल बाद उनकी उम्र मेरी उम्र से 3 गुना होगी। आठ साल पहले, मेरी उम्र और मेरे दादाजी की उम्र का अनुपात था ?

#12. अनुक्रम की संख्याएँ 52, 51, 48, 43, 34, 27, 16 एक पैटर्न बनाती हैं। उनमें से कौन सा पैटर्न में अनुपयुक्त है?

#13. यदि 80 व्यक्ति प्रतिदिन 6 घंटे काम करके किसी काम को 16 दिनों में पूरा कर सकते हैं, तो उसी काम को 15 दिनों में पूरा करने के लिए 64 व्यक्तियों को प्रतिदिन कितने घंटे काम करना होगा?
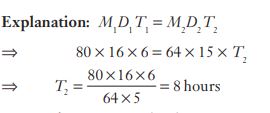
#14. दो संख्याओं का HCF और LCM क्रमशः 12 और 924 है। तो ऐसे युग्मों की संख्या है
Let the numbers be 12x and
12y where x and y are prime to
each other.
LCM = 12xy
12xy = 924
xy = 77
Possible pairs = (1,77) and (7,11)
#15. 12 के दो गुणजों का लघुत्तम समापवर्त्य 1056 है। यदि एक संख्या 132 है, तो दूसरी संख्या है

#16. एक पाइप एक टैंक को ‘x’ घंटे में भर सकता है और दूसरा पाइप इसे ‘y’ (y > x) घंटे में खाली कर सकता है। यदि दोनों पाइप खुले हैं, तो टैंक कितने घंटे में भर जाएगा?

#17. यदि प्रथम 50 क्रमागत धनात्मक पूर्णांकों का गुणनफल  से विभाज्य हो, जहाँ n एक पूर्णांक है, तो n का सबसे बड़ा संभावित मान क्या है?
से विभाज्य हो, जहाँ n एक पूर्णांक है, तो n का सबसे बड़ा संभावित मान क्या है?

#18. 8 मजदूर प्रतिदिन 9 घंटे काम करके 10 दिनों में 18 मीटर लंबी, 2 मीटर चौड़ी और 12 मीटर ऊंची दीवार बना सकते हैं। 6 घंटे प्रतिदिन काम करके 8 दिनों में 32 मीटर लंबी, 3 मीटर चौड़ी और 9 मीटर ऊंची दीवार बनाने में कितने मजदूर सक्षम होंगे?

#19. चार संख्याओं का औसत 60 है, उनमें से पहली संख्या अंतिम तीन संख्याओं के योग का एक-चौथाई है। पहली संख्या है|

#20. यदि रहीम ने लगातार 3 वर्षों की शुरुआत में बैंक में x रुपये की समान राशि जमा की और बैंक 5% प्रति वर्ष साधारण ब्याज देता है, तो तीसरे वर्ष के अंत में उसके खाते में राशि होगी|

#21.  बराबर है ?
बराबर है ?

#22. एक छात्र को एक दी गई संख्या को  से गुणा करने के लिए कहा गया था, इसके बजाय, उसने संख्या को
से गुणा करने के लिए कहा गया था, इसके बजाय, उसने संख्या को  से विभाजित किया। उसका उत्तर सही उत्तर से 225 अधिक था। दी गई संख्या थी?
से विभाजित किया। उसका उत्तर सही उत्तर से 225 अधिक था। दी गई संख्या थी?
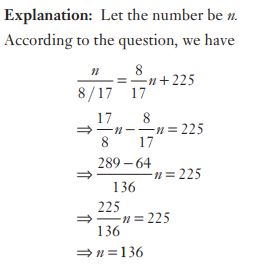
#23.  किसके बराबर है ?
किसके बराबर है ?

#24. 12 पंप प्रतिदिन 6 घंटे काम करके एक पूरी तरह से भरे जलाशय को 15 दिनों में खाली कर सकते हैं। ऐसे कितने पंप प्रतिदिन 9 घंटे काम करके उसी जलाशय को 12 दिनों में खाली कर देंगे?
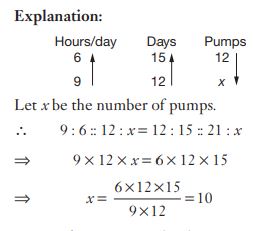
#25. एक धनराशि साधारण ब्याज की एक निश्चित दर पर 3 वर्षों में स्वयं की 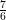 हो जाती है। प्रति वर्ष दर है:
हो जाती है। प्रति वर्ष दर है:

#26. यदि A और B दो बीजगणितीय अभिव्यक्तियों x और y के क्रमशः HCF और LCM हैं, और A + B = x + y हैं, तो  का मान है
का मान है
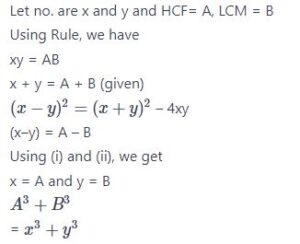
#27. अनुक्रम 0, 7, 26, 63, 124, 217 में विषम पद है ?

#28. एक क्रिकेट खिलाड़ी ने 10 टेस्ट खेलने के बाद 11वें टेस्ट में 100 रन बनाए। परिणामस्वरूप, उसके रनों का औसत 5 से बढ़ गया। रनों का वर्तमान औसत है|

#29. 400 और 800 के बीच कितनी संख्याएँ 4, 5 और 6 से विभाज्य हैं?

#30. एक पुरुष एक महिला से दोगुना तेज़ है और एक महिला एक लड़के से दोगुना तेज़ है। यदि वे सभी, एक पुरुष, एक महिला और एक लड़का 7 दिनों में काम पूरा कर सकते हैं, तो एक लड़का अकेले कितने दिनों में काम पूरा करेगा?

#31. एक अभ्यर्थी ने परीक्षा में 30% अंक प्राप्त किए और 6 अंकों से अनुत्तीर्ण हो गया। दूसरे अभ्यर्थी ने 40% अंक प्राप्त किए और उत्तीर्ण होने के लिए न्यूनतम आवश्यक अंक से 6 अंक अधिक प्राप्त किए। अधिकतम अंक हैं|

#32. वह बड़ी से बड़ी संख्या, जिससे 1657 और 2037 को भाग देने पर क्रमशः 6 और 5 शेष बचे, वह है
The largest number which when divide the numbers a, b and c give remainders as p, q, r respectively is given by HCF of (a – p), (b – q) and (c – r)
Required number
We have to find HCF of
(1657 – 6 = 1651) and (2037 – 5 = 2032)
1651 = 13 × 127, 2032 = 16 × 127
HCF = 127 So, required number will be 127
#33. यदि एक नाव धारा के अनुकूल 100 किमी 10 घंटे में तथा धारा के प्रतिकूल 75 किमी 15 घंटे में जाती है, तो धारा की गति है?

#34. हर रविवार को जिन 3 मील जॉगिंग करता है। सप्ताह के बाकी दिनों में, वह हर दिन पिछले दिन से 1 मील ज़्यादा जॉगिंग करता है। 2 सप्ताह में जिन कितने मील जॉगिंग करता है?
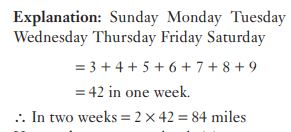
#35. एक नाव धारा के अनुकूल 12 किमी चलती है और 3 घंटे में प्रारंभिक बिंदु पर वापस आती है। यदि धारा की गति 3 किमी/घंटा है, तो स्थिर जल में नाव की गति (किमी/घंटा में) क्या है?

#36. तीन संख्याएँ 2 : 3 : 4 के अनुपात में हैं और उनका म.स.प. 12 है। संख्याओं का लघुत्तम समापवर्त्य है
Let the numbers be 2x, 3x and 4x respectively.
HCF = x = 12
Numbers are : 2 ×12 = 24
3 ×12 = 36, 4 ×12 = 48
LCM of 24, 36, 48
= 2 × 2 × 2 × 3 × 3 × 2 = 144
#37. साधारण ब्याज पर उधार दी गई एक धनराशि 2 वर्ष बाद 720 रुपये हो जाती है और 5 वर्ष बाद 1020 रुपये हो जाती है। मूलधन ज्ञात कीजिए।

#38. किसी वस्तु को 102 रुपये में बेचने पर 15% की हानि होती है, जबकि वस्तु को 134.40 रुपये में बेचा जाता है। लेन-देन में शुद्ध परिणाम है ?

#39. तीन साल पहले, 5 सदस्यों वाले एक परिवार की औसत आयु 17 वर्ष थी। एक बच्चे के जन्म के बाद, परिवार की औसत आयु आज भी वही है। बच्चे की वर्तमान आयु (वर्ष/वर्षों में) है|

#40. एक नल एक टंकी को 40 मिनट में भर सकता है तथा दूसरा नल भरी हुई टंकी को 60 मिनट में खाली कर सकता है। गलती से दूसरा नल बंद किए बिना ही पहला नल खोल दिया गया। खाली टंकी कितने मिनट में भर जाएगी?

#41. एक लड़का अपनी साइकिल 12 किमी/घंटा की औसत गति से 10 किमी चलाता है और फिर 10 किमी/घंटा की औसत गति से 12 किमी की यात्रा करता है। पूरी यात्रा के लिए उसकी औसत गति लगभग है ?

#42.  किसके बराबर है ?
किसके बराबर है ?
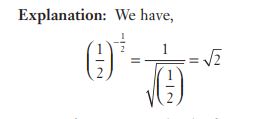
#43. जब  ) को
) को  ) से विभाजित किया जाता है, तो परिणाम प्राप्त होता है ?
) से विभाजित किया जाता है, तो परिणाम प्राप्त होता है ?

#44. चक्रवृद्धि ब्याज पर रखी गई एक धनराशि 4 वर्ष में दोगुनी हो जाती है। कितने वर्षों में यह राशि चार गुना हो जाएगी?
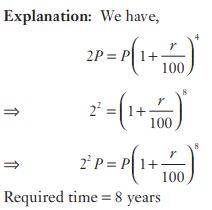
#45. एक व्यक्ति जो 4 पैसे प्रति रुपया की दर से आयकर का भुगतान करता है, पाता है कि ब्याज दर 4% से 3.75% तक गिरने से उसकी शुद्ध वार्षिक आय 48 रुपये कम हो जाती है। उसकी पूंजी क्या है?

#46. एक कस्बे में 1000 निवासियों में से 60% पुरुष हैं जिनमें से 20% साक्षर हैं। यदि सभी निवासियों में से 25% साक्षर हैं, तो कस्बे की कितनी प्रतिशत महिलाएँ साक्षर हैं?

#47. निम्नलिखित में से सबसे बड़ी भिन्न कौन सी है?

#48. 461+ 462 + 463 + 464 किससे विभाज्य है?

#49. एक टैंक का  भाग पानी से भरा है। जब 30 लीटर पानी निकाला जाता है, तो टैंक खाली हो जाता है। टैंक की क्षमता है |
भाग पानी से भरा है। जब 30 लीटर पानी निकाला जाता है, तो टैंक खाली हो जाता है। टैंक की क्षमता है |

#50. 7 से विभजित हो सकने वाली प्रथम छह विषम संख्याओं का औसत क्या है |