HCF and LCM Questions for Competitive Exams in Hindi

HCF and LCM Questions with answers and solution for SSC CGL, CHSL, GD Competitive Exams in Hindi. Mock Test for free online practice of Maths MCQs for upcoming exams.

मॉक टेस्ट : HCF और LCM
माध्यम : हिंदी
विषय : गणित
पिछले वर्ष के परीक्षा पत्र से सभी प्रकार के प्रश्न
शॉर्ट ट्रिक्स के साथ उत्तर और समाधान

Results

#1. वह बड़ी से बड़ी संख्या, जिससे 122 और 243 को भाग देने पर क्रमश: 2 और 3 शेष बचता है, वह है

120

Clearly, 122 – 2 = 120 and 243 – 3 = 240 are exactly divisible by the required number.
Required number
= HCF of 120 and 240 = 120

#2. दो संख्याओं का HCF और LCM क्रमशः 21 और 84 है। यदि दो संख्याओं का अनुपात 1 : 4 है, तो दोनों संख्याओं में बड़ी संख्या है

108

HCF of numbers = 21
Numbers = 21x and 21y
Where x and y are prime to each other.
Ratio of numbers = 1 : 4
Larger number = 21 × 4 = 84

#3. वह छोटी से छोटी संख्या जिसे 36798 में से घटाने पर 78 से पूर्णतः विभाजित होने वाली संख्या प्राप्त हो

When 36798 is divided by 78, remainder = 60
The least number to be subtracted = 60

#4. दो संख्याओं का लघुत्तम समापवर्तक 1920 है और उनका उच्चतम समापवर्तक 16 है। यदि एक संख्या 128 है, तो दूसरी संख्या ज्ञात कीजिए।

204

240

260

320

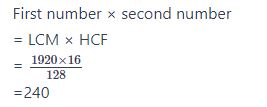
#5. दो संख्याओं का HCF और LCM क्रमशः 12 और 924 है। तो ऐसे युग्मों की संख्या है

Let the numbers be 12x and
12y where x and y are prime to
each other.
LCM = 12xy
12xy = 924
xy = 77
Possible pairs = (1,77) and (7,11)

#6. एच सी एफ. दो संख्याओं का लघुत्तम समापवर्त्य 96 है और उनका लघुत्तम समापवर्त्य 1296 है। यदि एक संख्या 864 है, तो दूसरी है

132

135

140

144

#7. दो सह-अभाज्य संख्याओं का गुणनफल 117 है। तो उनका लघुत्तम समापवर्त्य है

117

HCF of two-prime numbers = 1
Product of numbers = their
LCM = 117
117 = 13 × 9 where 13 & 9 are
co-prime. L.C.M (13,9) = 117

#8. दो संख्याओं का उच्चतम समापवर्तक 8 है। निम्नलिखित में से कौन-सा एक उनका लघुत्तम समापवर्त्य कभी नहीं हो सकता है?

दो संख्याओं का एचसीएफ 8 है। इसका मतलब है कि 8 दोनों संख्याओं के लिए सामान्य कारक है। लघुत्तम समापवर्त्य दो संख्याओं का समापवर्तक है, यह दो संख्याओं से विभाज्य है। अत: अभीष्ट उत्तर = 60

#9. सबसे छोटी संख्या जिसे 4, 6, 8, 12 और 16 से भाग देने पर प्रत्येक स्थिति में 2 शेष बचता है:

L.C.M. of 4, 6, 8, 12 and 16 = 48
Required number = 48 2 = 50

#10. चार अंकों की सबसे बड़ी संख्या ज्ञात कीजिए जिससे 15,18, 21 तथा 24 से भाग देने पर शेषफल क्रमशः 11, 14, 17 तथा 20 हो।

6557

7556

5675

7664

#11. सबसे छोटा पूर्ण वर्ग, जो 21, 36 और 66 में से प्रत्येक से विभाज्य है

214344

214434

213444

231444

#12. वह सबसे छोटी संख्या कौन सी है जिसे 5, 6 या 8 में से किसी संख्या से विभाजित करने पर 3 शेष बचता है लेकिन 9 से विभाजित करने पर कोई शेष नहीं रहता है?

123

603

723

243

#13. 1936 में से कौन सी सबसे छोटी संख्या घटाई जाए कि परिणामी संख्या को 9, 10 और 15 से विभाजित करने पर प्रत्येक स्थिति में वही शेषफल 7 बचे?

LCM of 9, 10 and 15 = 90
The multiple of 90 are also divisible by 9, 10 or 15.
21 × 90 = 1890 will be divisible by them.
Now, 1897 will be the number
that will give remainder 7.
Required number = 1936 – 1897 = 39

#14. वह बड़ी से बड़ी संख्या, जिससे 989 और 1327 को भाग देने पर क्रमश: 5 और 7 शेष बचता है, वह है

The largest number which when divide the numbers a, b and c give remainders as p, q, r respectively is given by H.C.F. of (a – p), (b – q) and (c – r)
Required number
= HCF of (989 – 5) and (1327 – 7)
= HCF of 984 and 1320 = 24
HCF = 24

#15. HCF of $\frac {2}{3} , \frac{4}{5} and \frac{6}{7}$ is

$ \frac{48}{105} $

$ \frac{2}{105} $

$ \frac{1}{105} $

$ \frac{24}{105} $

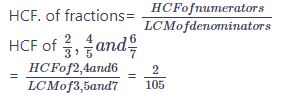
#16. वह बड़ी से बड़ी संख्या, जिससे 1657 और 2037 को भाग देने पर क्रमशः 6 और 5 शेष बचे, वह है

127

133

235

305

The largest number which when divide the numbers a, b and c give remainders as p, q, r respectively is given by HCF of (a – p), (b – q) and (c – r)
Required number
We have to find HCF of
(1657 – 6 = 1651) and (2037 – 5 = 2032)
1651 = 13 × 127, 2032 = 16 × 127
HCF = 127 So, required number will be 127

#17. 84 गणित की किताबें, 90 फिजिक्स की किताबें और 120 केमिस्ट्री की किताबों को टॉपिक वाइज स्टैक करना है। प्रत्येक ढेर में कितनी किताबें होंगी ताकि प्रत्येक ढेर की ऊँचाई भी समान हो ?

As the height of each stack is same, the required number of books in each stack
HCF of 84, 90 and 120
84 = 2 × 2 × 3 × 7, 90 = 2 × 3 × 3 × 5, 120 = 2 × 2 × 2 × 3 × 5
HCF = 2 × 3 = 6

#18. दो 2-अंकीय संख्याओं का गुणनफल 2160 है और उनका HCF 12 है। संख्याएँ हैं

(12, 60)

(72, 30)

(36, 60)

(60, 72)

#19. यदि दो संख्याओं का अनुपात 2 : 3 है और उनका लघुत्तम समापवर्त्य 54 है, तो दो संख्याओं का योग है

270

Let the two numbers are 2x and 3x respectively.
According to question,
LCM = 54
x (3×2)=54
x = 9
Numbers = 2x = 2 × 9 = 18 and 3x = 3 × 9 = 27
Sum of the two numbers
= 18 27 = 45

#20. तीन संख्याएँ 2 : 3 : 4 के अनुपात में हैं और उनका म.स.प. 12 है। संख्याओं का लघुत्तम समापवर्त्य है

144

192

Let the numbers be 2x, 3x and 4x respectively.
HCF = x = 12
Numbers are : 2 ×12 = 24
3 ×12 = 36, 4 ×12 = 48
LCM of 24, 36, 48
= 2 × 2 × 2 × 3 × 3 × 2 = 144

#21. दो संख्याएँ 3 : 4 के अनुपात में हैं। उनका लघुत्तम समापवर्त्य 84 है। बड़ी संख्या है

#22. तीन संख्याएँ 1 : 2 : 3 के अनुपात में हैं और उनका उच्चतम समापवर्तक 12 है। संख्याएँ हैं

12, 24, 36

5, 10, 15

4, 8, 12

10, 20, 30

Numbers = x , 2 x and 3 x (let)
Their HCF = x = 12
Numbers = 12, 24 and 36

#23. दो संख्याओं के अधिकतम समापवर्तक और लघुतम समापवर्त्य का योग 680 है और लघुत्तम समापवर्त्य सबसे बड़े समापवर्तक का 84 गुना है। यदि एक संख्या 56 है, तो दूसरी संख्या है:

#24. सकारात्मक पूर्णांक की एक जोड़ी का योग 336 है और उनका एच.सी.एफ 21 है। ऐसे संभावित जोड़े की संख्या है

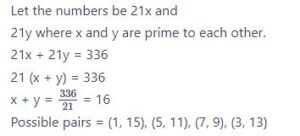
#25. दो संख्याओं के लघुतम समापवर्त्य और सबसे बड़े समापवर्तक का गुणनफल 24 है। यदि संख्याओं का अंतर 2 है, तो बड़ी संख्या है

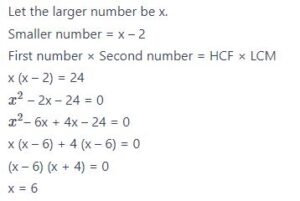
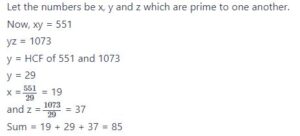
#26. तीन संख्याएँ जो एक दूसरे की सहअभाज्य हैं, इस प्रकार हैं कि पहले दो का गुणनफल 551 है और अंतिम दो का गुणनफल 1073 है। तीन संख्याओं का योग है:

#27. यदि A और B दो बीजगणितीय अभिव्यक्तियों x और y के क्रमशः HCF और LCM हैं, और A + B = x + y हैं, तो $A^3+B^3$ का मान है

$ x^3 -y^3 $

$ x^3 $

$ y^3 $

$ x^3 +y^3 $

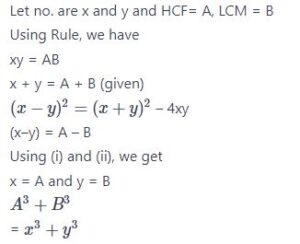
#28. 12 के दो गुणजों का लघुत्तम समापवर्त्य 1056 है। यदि एक संख्या 132 है, तो दूसरी संख्या है

132

#29. 23 का वह लघुतम गुणज ज्ञात कीजिए जिसे 18, 21 और 24 से भाग देने पर क्रमशः 7, 10 और 13 शेष बचता है।

3013

3024

3002

3036

LCM of 18, 21 and 24
LCM = 2 × 3 × 3 × 7 × 4 = 504
Now compare the divisors with their respective remainders. We observe that in all the cases the remainder is just 11 less than their respective divisor. So the number can be given by 504 K – 11 Where K is a positive integer
Since 23 × 21 = 483
We can write 504 K – 11
= (483 21) K – 11, = 483 K (21K – 11)
483 K is multiple of 23, since 483 is divisible by 23.
So, for (504K – 11) to be multiple of 23, the remainder (21K – 11) must be divisible by 23.
Put the value of K = 1, 2, 3, 4, 5,6, ….. and so on successively.
We find that the minimum value of K for which (21K – 11) is divisible by 23. is 6, (21 × 6 – 11)
= 115 which is divisible by 23.
Therefore, the required least number
= 504 × 6 – 11 = 3013

#30. a, b का उच्चतम समापवर्तक 12 है, a, b धनात्मक पूर्णांक हैं और a > b > 12. (a, b) के सबसे छोटे मान क्रमशः हैं

12, 24

24, 12

24, 36

36, 24

HCF of a and b = 12
Numbers = 12x and 12y where x and y are prime to each other.
a > b > 12
a = 36; b = 24

FINISH