Mensuration Questions for SSC with Answer and Solutions – Mock Test for free online practice. Previous year MCQs from of SSC CGL, CHSL, CPO, GD Competitive Exams.
Mock Test : Mensuration Questions
Subject : Mathematics
Medium : English
Important MCQs from the previous year SSC Papers
All type of questions with short tricks and explanation
Results
#1. The amount of rice produced in a square field of side 50 m is 750 kg. The amount of rice produced in a similar square field of side 100 m will be

#2. The volume of air in a room is 204 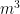 The height of the room is 6 m. What is the floor area of the room?
The height of the room is 6 m. What is the floor area of the room?

#3. A hall 25 metres long and 15 metres broad is surrounded by a veranda of uniform width of 3.5 metres. The cost of flooring the veranda at 27.50 per square metre is

#4. If water is freezed to become ice, its volume is increased by 10% and then if the ice is melted to water again, then its volume will be decreased by

#5. The diagonals of two squares are in the ratio of 3 : 7. What is the ratio of their areas?

#6. What will be the percentage of increase in the area square when each of the its sides is increased by 10%?

#7. If the length of each of two equal sides of an isosceles triangle is 10 cm and the adjacent angle is 45°, then the area of the triangle is :

#8. The length of the diagonal of a rectangle with sides 4 m and 3 m would be

#9. Two isosceles triangles have equal vertical angles and their areas are in the ratio of 9 : 16. Then the ratio of their corresponding heights is :

#10. If the altitude of an equilateral triangle is  cm, then its area would be :
cm, then its area would be :

#11. A plate on square base made of brass is of length  cm and width 1 mm. The plate weighs 4725 gm. If 1 cubic cm of brass weighs 8.4 gram, then the value of
cm and width 1 mm. The plate weighs 4725 gm. If 1 cubic cm of brass weighs 8.4 gram, then the value of  is :
is :

#12. The perimeter of a triangle is 54 m and its sides are in the ratio of 5 : 6 : 7 The area of the triangle is

#13. The lengths of two parallel sides of a trapezium are 6 cm and 8 cm. If the height of the trapezium be 4 cm, then its area is :

#14. If the sides of an equilateral triangle be increased by 1 m its area is increased by 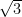 sq. metre. The length of any of its sides is
sq. metre. The length of any of its sides is

#15. The perimeter of a triangle and an equilateral triangle are same. Also, one of the sides of the rectangle is equal to the side of the triangle. The ratio of the area of the rectangle and the triangle is :

#16. If the sum of the length, breadth and height of a rectangular parallelepiped is 24 cm and the length of its diagonal is 15 cm, then its total surface area is

#17. The radii of two circles are 10 cm and 24 cm. The radius of a circle whose area is the sum of the area of these two circles is

#18. The perimeter of a semi-circular path is 36 m. Find the area of this semi-circular path.

#19. The four equal circles of radius 4 cm drawn on the four corners of a square touch each other externally. Then the area of the portion between the square and the four sectors is

#20. The area of an equilateral triangle is  The length of each side of the triangle is
The length of each side of the triangle is

#21. If the area of a circle inscribed in a square is  , then the area of the square is
, then the area of the square is

#22. If the circumference of a circle is reduced by 50%, its area will be reduced by :

#23. A took 15 sec to cross a rectangular field diagonally walking at the rate of 52 m/min. and B took the same time to cross the same field along its sides walking at the rate of 68 m/min. The area of the field is

#24. If the length of a rectangle is increased by 25% and the width is decreased by 20%, then the area of the rectangle

#25. The sides of a triangle having area 7776 sq. cm are in the ratio 3 : 4 : 5. The perimeter of the triangle is :

#26. The in-radius of an equilateral triangle is 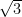 cm, then the perimeter of that triangle is .
cm, then the perimeter of that triangle is .

#27. The diameter of a wheel is 98 cm. The number of revolutions in which it will have to cover a distance of 1540 m is :

#28. The ratio of the radii of two wheels is 3 :4 The ratio of their circumference is
Explanation: Tricky Approach
Ratio of the circumference
= Ratio of radii = 3 : 4
#29. The ratio of the numbers giving the measure of the circumference and the area of a circle of radius 3 cm is

#30. If the area of a circle and a square are equal, then the ratio of their perimeter is

#31. The area of a circle is 38.5 sq. cm. Its circumference (in cm) is (use 

#32. If each edge of a square be doubled, then the increase percentage in its area is :

#33. A prism with a right triangular base is 25 cm high. If the shorter sides of the triangle are in the ratio of 1 : 2 and volume of the prism is 100 cm3, what is the length of the longest side of the triangle?

#34. Length of each edge of a regular tetrahedron is 1 cm. It volume is

#35. A right triangle with sides 9 cm, 12 cm and 15 cm is rotated about the side of 9 cm to form a cone. The volume of the cone so formed is

#36. The height of a prism-shaped part of a machine is 8 cm and its base is an isosceles triangle, whose each of the equal sides is 5 cm and remaining side is 6 cm. The volume of the part is

#37. A right pyramid 6 m height has a square base of which the diagonal is  m . Volume of the pyramid is
m . Volume of the pyramid is

#38. A rectangular piece of paper of dimensions 22 cm by 12 cm is rolled along its length to form a cylinder. The volume (in cu. cm) of the cylinder so formed is (Take  )
)

#39. The curved surface area and the total surface area of a cylinder are in the ratio 1 : 2. If the total surface area of the right cylinder is 616  , then its volume is
, then its volume is

#40. The perimeter of the base of a right circular cone is 8 cm. If the height of the cone is 21 cm, then its volume is

#41. A semi-circular sheet of metal of diameter 28 cm is bent into an open conical cup. The capacity of the cup (taking  ) is
) is

#42. A solid sphere is melted and recast into a right circular cone with a base radius equal to the radius of sphere. What is the ratio of the height and radius of the cone so formed?

#43. From a solid cylinder whose height is 12 cm and diameter 10 cm, a conical cavity of same height and same diameter of the base is hollowed out. The volume of the remaining solid is approximately  )
)

#44. If the radii of the circular ends of a truncated conical bucket which is 45 cm high be 28 cm and 7 cm, then the capacity of the bucket in cubic centimetre is (Take  )
)

#45. If the height of a cone is increased by 100% then its volume is increased by

#46. A copper rod of 1 cm diameter and 8 cm length is drawn into a wire of uniform diameter and 18 m length. The radius (in cm) of the wire is

#47. The length, breadth and height of a wooden box with a lid are 10 cm, 9 cm and 7 cm respectively. The total inner surface of the closed box is 262  . The thickness of the wood (in cm) is
. The thickness of the wood (in cm) is

#48. The diameter of a 120 cm long roller is 84 cm. It takes 500 complete revolutions of the roller to level a ground. The cost of levelling the ground at Rs. 1.50 per sq. metre is

#49. The volume of a cubical box is 3.375 cubic metres. The length of edge of the box is

#50. The diameter of two hollow spheres made from the same metal sheet is 21 cm and 17.5 cm respectively. The ratio of the area of metal sheets required for making the two spheres is

#51. A cuboidal block of 6 cm × 9 cm × 12 cm is cut up into exact number of equal cubes. The least possible number of cubes will be
