CUET UG Mathematics Mock Test for free online practice of entrance exam 2025-2026.
Subject: Mathematics
Medium: English
Questions: 50
Results
#1. Let n(A) = 4 and n(B) = 6. Then, the number of one-one functions from A to B is
#2. A relation R from A to B is an arbitrary subset of
#3. Let A = {1, 2, 3}. Then, number of relations containing (1, 2) and (1, 3) which are reflexive and symmetric but not transitive, is
#4. Let f : R – 
 R be a function defined as f[x]=
R be a function defined as f[x]=  The inverse of f is the map g : range f
The inverse of f is the map g : range f 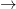 R –
R –  given by
given by
#5. The domain in which sine function will be one-one, is
#6. cosec x is not defined for
#7. The principal value of  is
is
#8. The value of  is ……. Here, X refers to
is ……. Here, X refers to
#9. The number of all possible matrices of order 3 x 3 with each entry 0 or 1 is
#10. If A and B are two matrices of the order 3 x m and 3 x n, respectively and m=n, then the order of the matrix (5A – 2B)is
#11. Two matrices A = [aij] and B =[bij] are said to be equal, if they are of same order and for all i and j
#12. If A is a 3 x 2 matrix, B is a 3 x 3 matrix and C is a 2 x 3 matrix, then the elements in A, B and C are respectively
#13. The area of the triangle, whose vertices are (3, 8), (-4, 2) and (5, 1), is
#14. If each element of a row (or a column) of a determinant is multiplied by a constant k, then its value gets …A… by k. Here, A refers to
#15. If the value of the determinant  is positive, then
is positive, then
#16. If  , then the cofactor
, then the cofactor 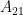 is
is
#17. The function  is not continuous at
is not continuous at
#18. Continuity of a function at a point is entirely dictated by the…A… of the function at that point. Here, A refers to
#19. A function is said to be differentiable in an interval [a, b ], if it is differentiable at every point of [a, b ]
#20. Let b > 1be a real number. Then, logarithm of a to the base b is x, if
#21. The radius of a circle is increasing uniformly at the rate of 3 cm/s. At radius of 10 cm, the area of the circle is increasing at the rate of
#22. The function given f(x)=e2x is …A… on R. Here, A refers to
#23. The function given by f(x) = x3 – 3x2 + 3x – 100 is
#24. The approximate value of f(2.01), if f(x) =4x2 + 5x + 2, is
#25. If the derivative of a function sec-1x is  then the anti-derivative of
then the anti-derivative of  is
is
#26. The anti-derivative of [ sec x (sec x + tan x)] is
#27. The integral of the function tan4 x is
#28. The value of  is
is
#29. If the area between x = y2 and x = 4 is divided into two equal parts by the line x = a, then the value of a is
#30. Area of the region bounded by the curve y = cos x between x = 0 and x = 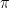 is
is
#31. Area (in sq units) lying between the curves y2 = 4x and y = 2x is
#32. The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is
#33. The equation of the form  =0 is a\an
=0 is a\an
#34. The equation y = mx + c, where m and c are parameters, represents family of
#35. The equation of a curve whose tangent at any point on it different from origin has slope  is
is
#36. A differential equation of the form  =F(x, y) is said to be homogeneous, if F(x, y) is a homogeneous function of degree
=F(x, y) is said to be homogeneous, if F(x, y) is a homogeneous function of degree
#37. If two or more vectors are parallel to the same line then they are called
#38. If four points A(3,2,1), B(4, x, 5), C (4,2,-2) and D (6, 5,-1) are coplanar, then the value of x is
