Simplification Questions with Solutions – Free MCQs Mock Test for online practice of competitive exams.
Quiz : Maths – Simplification
Medium – English
All type solved questions.
Selected from previous year SSC papers
Results
#1.  is equal to
is equal to

#2. The square of a natural number subtracted from its cube is 48. The number is

#3. The value of  is
is
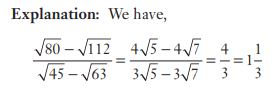
#4. The sum of two numbers is 37 and the difference of their squares is 185, then the difference between the two numbers is :

#5. The value of is 
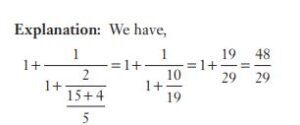
#6. The value of 

#7. The value of  is
is

#8. Find the value of 
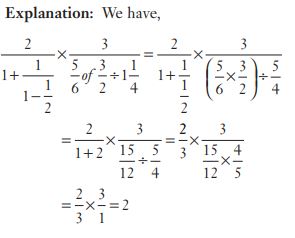
#9. The simplified value of  is
is
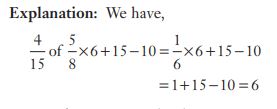
#10. The value of ![3\div[\left(8-5)\div{\{(4-2)+(2+\frac{8}{13})}\}\right]](https://s0.wp.com/latex.php?latex=3%5Cdiv%5B%5Cleft%288-5%29%5Cdiv%7B%5C%7B%284-2%29%2B%282%2B%5Cfrac%7B8%7D%7B13%7D%29%7D%5C%7D%5Cright%5D++&bg=ffffff&fg=000&s=0&c=20201002) is
is
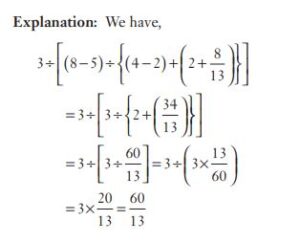
#11. The value of ![3\frac12 -[2\frac14+ \{{1\frac14-\frac12(1\frac12-\frac13-\frac16)}\}]](https://s0.wp.com/latex.php?latex=3%5Cfrac12+-%5B2%5Cfrac14%2B+%5C%7B%7B1%5Cfrac14-%5Cfrac12%281%5Cfrac12-%5Cfrac13-%5Cfrac16%29%7D%5C%7D%5D+&bg=ffffff&fg=000&s=0&c=20201002) is
is
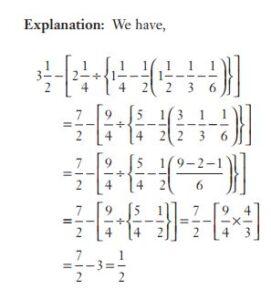
#12. The value of  is
is

#13.  is simplified to
is simplified to
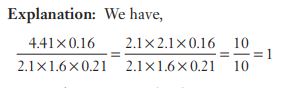
#14.  is equal to
is equal to

#15. The simplification of  up to three places of decimals yields
up to three places of decimals yields
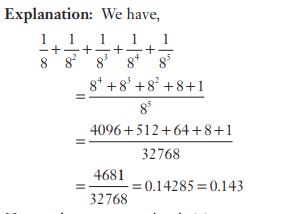
#16. if =80, then P is equal to
=80, then P is equal to
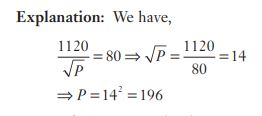
#17. the value of 25 – 5 [2 + 3 (2 – 2 (5 – 3) + 5) – 10] ÷ 4 is
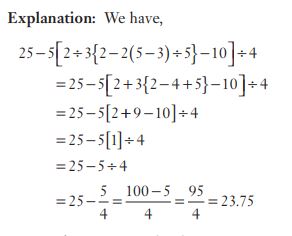
#18. When ) is divided by
) is divided by  ), the result is
), the result is

#19. 5 – [4 – (3 – (3 – 3 – 6))] is equal to
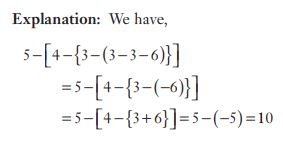
#20. The value of ( is
is
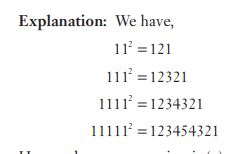
#21. The least number which must be added to 1728 to make it a perfect square is :
#22. if  = 12122101, then find the value of
= 12122101, then find the value of 
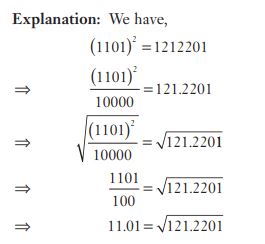
#23. The square root of 

#24.  is equal to
is equal to
#25. the simplified value of  is
is

#26. The number, whose square is equal to the difference between the squares of 975 and 585 is :

#27.  +
+ is equal to
is equal to
#28. The least number, that must be added to 1720 so as to obtain a perfect cube is :

#29. The sum of the cubes of the numbers 22, -15 and -7 is equal to
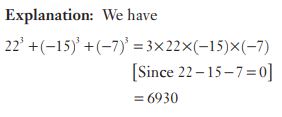
#30. ![\sqrt[3]{(333)^3+(333)^3+(334)^3 -3\times333\times333\times334}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B%28333%29%5E3%2B%28333%29%5E3%2B%28334%29%5E3+-3%5Ctimes333%5Ctimes333%5Ctimes334%7D+&bg=ffffff&fg=000&s=0&c=20201002) is equal to
is equal to
