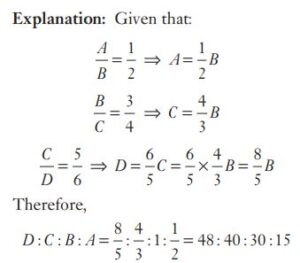Algebra Questions for SSC CGL, CHSL, CPO with answers and solutions in English. MCQs Mock Test for online practice of Competitive Exams.
Quiz : Algebra
Subject : Mathematics
Solved Objective Questions from the previous year papers
Results
#1. If  =
= , the value of
, the value of  )is
)is

#2. If a, b, c are real numbers and  = 2 (a − b − c) − 3, then the value of a + b + c is
= 2 (a − b − c) − 3, then the value of a + b + c is
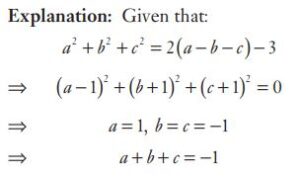
#3. If a = , then the value of
, then the value of  ) is
) is

#4. If  = ab + bc + ca, then the value of
= ab + bc + ca, then the value of  is
is

#5.  can be expressed as the square of
can be expressed as the square of
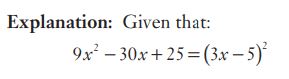
#6. If  , then the value of (a – b) is
, then the value of (a – b) is
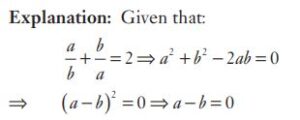
#7. If  , then
, then  is
is
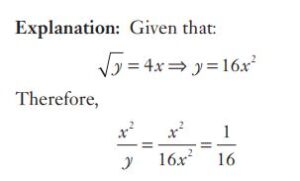
#8. If a + b = 1, c + d = 1 and a – b =  , then the value of
, then the value of  is :
is :

#9. If  is a factor of
is a factor of  , then the value of Q is :
, then the value of Q is :
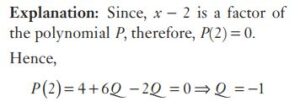
#10. If  , then the value of
, then the value of  is
is

#11. If  , then the value of
, then the value of  is
is
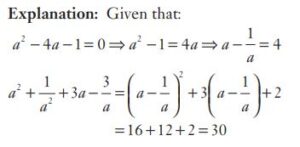
#12. If  and
and  , then the average of
, then the average of  and
and 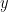 is
is
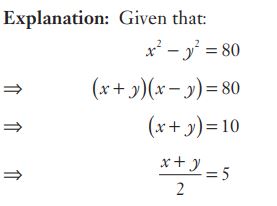
#13. If  , then
, then  is
is
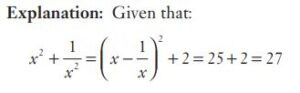
#14. If  , then the value of
, then the value of  is
is
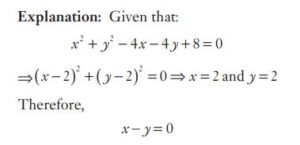
#15. If  , then the value of
, then the value of  is
is
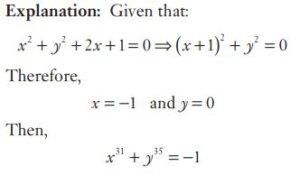
#16. If  and
and  , then the value of
, then the value of  is
is

#17. If  , then the value of n is :
, then the value of n is :
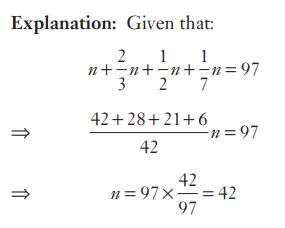
#18. If  , then
, then  equals
equals
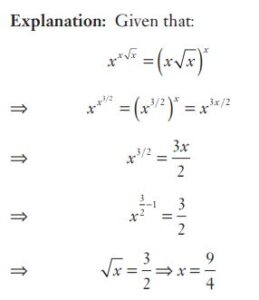
#19. If  , then the value of
, then the value of  is
is
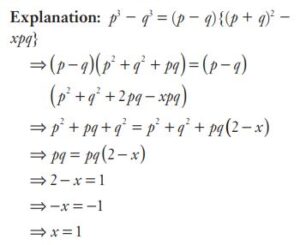
#20. If  , then the value of
, then the value of  is
is

#21. If  , then the value of
, then the value of  is
is

#22. If  and
and  , then the value of
, then the value of  is
is

#23. The simplified value of the following is : 

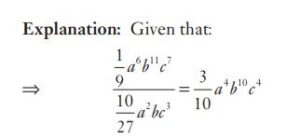
#24. If  , then the value of
, then the value of  is
is
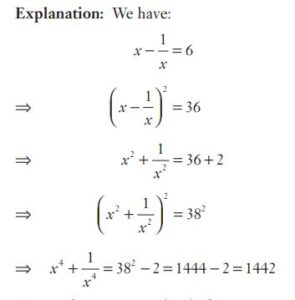
#25. If  , then the value of
, then the value of  is
is
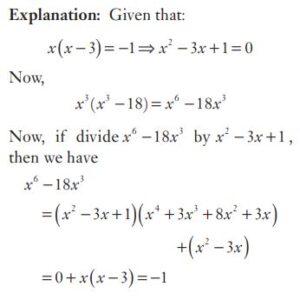
#26. If  , then the value of
, then the value of  is
is

#27. If  and
and  , then the value of
, then the value of  will be
will be

#28. If  and
and  , then
, then  =
=
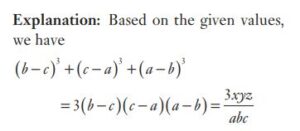
#29. If a/b = 1/2, then find the value of the expression (2a − 5b)/(5a + 3b)
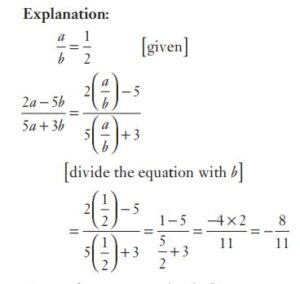
#30. If  , then
, then  is
is

#31. If A : B = 1 : 2, B : C = 3 : 4 and C : D = 5 : 6, find D : C : B : A