CUET (UG) Mathematics Sample Paper

Common University Entrance Test – CUET (UG) Mathematics Sample Paper as per official syllabus and exam pattern. CUET exam Section II Domain Subject Maths paper Mock for free online practice for the admission in 2024 – 2025 Academic session.

CUET (UG) Sample Paper : Mathematics

Instruction : Attempt any 40 questions out of 50
Duration : 45 Minutes

Q1: Let n(A) = 4 and n(B) = 6. Then, the number of one-one functions from A to B is
(a) 24
(b) 60
(c) 120
(d) 360

Show Answer

Ans : (d) 360

Q.2: A relation R from A to B is an arbitrary subset of
(a) A x B
(b) B x A
(c) A x A
(d) B x B

Show Answer

Ans : (a) A x B

Q.3: Let A = {1, 2, 3}. Then, number of relations containing (1, 2) and (1, 3) which are reflexive and symmetric but not transitive, is
(a) 1
(b) 2
(c) 3
(d) 4

Show Answer

Ans : (a) 1

Q.4: Let $f : R - \{-\frac43\} \rightarrow$ R be a function defined as $f[x]=\frac{4x}{3x+4}$ The inverse of f is the map g : range $f \rightarrow R -\{-\frac43\}$ given by
(a) $g(y) =\frac{3y}{3-4y}$
(b) $g(y) =\frac{4y}{4-3y}$
(c) $g(y) =\frac{4y}{3-4y}$
(d) $g(y) =\frac{3y}{4-3y}$

Show Answer

Ans : (b) $g(y) =\frac{4y}{4-3y}$

Q.5: The domain in which sine function will be one-one, is
(a) $[\frac{-\pi}{2},\frac{\pi}{2}]$
(b) $[\frac{\pi}{2},\frac{3\pi}{2}]$
(c) $[0,\pi]$
(d) Both (a) and (b)

Show Answer

Ans : (d) Both (a) and (b)

Q.6: cosec x is not defined for
(a) all integral multiples of $\frac{\pi}{2}$
(b) all integral multiples of $\pi$
(c) all integral multiples of $\frac{3\pi}{4}$
(d) None of the above

Show Answer

Ans : (b) all integral multiples of $\pi$

Q.7: The principal value of $cos^{-1} (\frac12)-2sin^{-1}(-\frac{1}{2})$ is
(a) $\frac \pi3$
(b) $\frac{-\pi}{3}$
(c) $\frac {2\pi}{3}$
(d) $\frac \pi6$

Show Answer

Ans : (c) $\frac {2\pi}{3}$

Q.8: The value of $sin^1(sin\frac{2\pi}{3})$ is ……. Here, X refers to
(a) $\frac\pi2$
(b) $\frac\pi6$
(c) $\frac\pi3$
(d) 0

Show Answer

Ans : (c) $\frac\pi3$

Q.9: The number of all possible matrices of order 3 x 3 with each entry 0 or 1 is
(a) 27
(b) 18
(c) 81
(d) 512

Show Answer

Ans : (d) 512

Q.10: If A and B are two matrices of the order 3 x m and 3 x n, respectively and m=n, then the order of the matrix (5A – 2B)is
(a) m x 3
(b) 3 x 3
(c) m x n
(d) 3 x n

Show Answer

Ans : (d) 3 x n

Q.11: Two matrices A = [a_ij] and B =[b_ij] are said to be equal, if they are of same order and for all i and j
(a) a_ij = b_ji
(b) a_ij = b_ij
(c) a_ij = – b_ij
(d) a_ij + b_ij = 0

Show Answer

Ans : (b) a_ij = b_ij

Q.12: If A is a 3 x 2 matrix, B is a 3 x 3 matrix and C is a 2 x 3 matrix, then the elements in A, B and C are respectively
(a) 6, 9, 8
(b) 6, 9, 6
(c) 9, 6, 6
(d) 6, 6, 9

Show Answer

Ans : (b) 6, 9, 6

Q.13: The area of the triangle, whose vertices are (3, 8), (-4, 2) and (5, 1), is
(a) 60
(b) 61
(c) $\frac{61}{2}$
(d) 30

Show Answer

Ans : (c) $\frac{61}{2}$

Q.14: If each element of a row (or a column) of a determinant is multiplied by a constant k, then its value gets …A… by k. Here, A refers to
(a) added
(b) subtracted
(c) divided
(d) multiplied

Show Answer

Ans : (d) multiplied

Q.15: If the value of the determinant $\begin {vmatrix} a & 1 & 1 \\ 1 & b & 1 \\ 1 & 1 & c \end {vmatrix}$ is positive, then
(a) abc > 1
(b) abc > – 8
(c) abc < – 8
(d) abc > – 2

Show Answer

Ans : (b) abc > – 8

Q.16: If $\triangle = \begin{vmatrix} a & h & g \\ h & b & f \\ g & f & c\end {vmatrix}$ , then the cofactor A₂₁ is
(a) -(hc + fg)
(b) fg – hc
(c) fg + hc
(d) hc – fg

Show Answer

Ans : (b) fg – hc

Q.17: The function $f(x)=\begin{Bmatrix} 1, \text{if x} \neq 0 \\ 2 , \text{if x} = 0\end{Bmatrix}$ is not continuous at
(a) x = 0
(b) x = 1
(c) x = -1
(d) None of these

Show Answer

Ans : (a) x = 0

Q.18: Continuity of a function at a point is entirely dictated by the…A… of the function at that point. Here, A refers to
(a) limit
(b) value
(c) Both (a) and (b)
(d) None of these

Show Answer

Ans : (c) Both (a) and (b)

Q.19: A function is said to be differentiable in an interval [a, b ], if it is differentiable at every point of [a, b ]
(a) including a and b
(b) excluding a and b
(c) including a but not b
(d) including b but not a

Show Answer

Ans : (a) including a and b

Q.20: Let b > 1be a real number. Then, logarithm of a to the base b is x, if
(a) b^a = x
(b) a^b = x
(c) b^x = a
(d) None of these

Show Answer

Ans : (c) b^x = a

Q.21: The radius of a circle is increasing uniformly at the rate of 3 cm/s. At radius of 10 cm, the area of the circle is increasing at the rate of
(a) $20\pi$ cm²/ S
(b) $40\pi$ cm²/ S
(c) $60\pi$ cm²/ S
(d) $80\pi$ cm²/ S

Show Answer

Ans : (d) $80\pi$ cm²/ S

Q.22: The function given f(x)=e^2x is …A… on R. Here, A refers to
(a) strictly increasing
(b) strictly decreasing
(c) neither increasing nor decreasing
(d) decreasing

Show Answer

Ans : (a) strictly increasing

Q.23: The function given by f(x) = x³ – 3x² + 3x – 100 is
(a) increasing on R
(b) decreasing on R
(c) strictly decreasing on R
(d) None of these

Show Answer

Ans : (a) increasing on R

Q.24: The approximate value of f(2.01), if f(x) =4x² + 5x + 2, is
(a) 28.21
(b) 18.24
(c) 21.28
(d) 29.30

Show Answer

Ans : (a) 28.21

Q.25: If the derivative of a function sec^-1x is $\frac{1}{x\sqrt{x^2 - 1}}$ , then the anti-derivative of $\frac{1}{x\sqrt{x^2 - 1}}$ is
(a) sec^-1 x
(b) sec^-1x+C
(c) 2 sec^-1x
(d) None of these

Show Answer

Ans : (b) sec^-1x+C

Q.26: The anti-derivative of [ sec x (sec x + tan x)] is
(a) 2sec x + C
(b) tan x + sec x + C
(c) sec² x + sec x tan x + C
(d) None of these

Show Answer

Ans : (b) tan x + sec x + C

Q.27: The integral of the function tan⁴ x is
(a) $\frac{\text{tan}^3x}{3}-\text{tan}x-x+C$
(b) $\frac{\text{tan}^3x}{3}+\text{tan}x-x+C$
(c) $\frac{\text{tan}^3x}{3}-\text{tan}x+x+C$
(d) $\frac{\text{tan}^3x}{3}+\text{tan}x+x+C$

Show Answer

Ans : (c) $\frac{\text{tan}^3x}{3}-\text{tan}x+x+C$

Q.28: The value of $\frac{1}{\sqrt{7-6x-x^2}}$ is
(a) $\text{log}[2x + \sqrt{7 - 6x - x^2}]+C$
(b) $\frac12\text{log}\begin{vmatrix} \frac {x+3}{x-3}\end{vmatrix}+C$
(c) sin^-1 $(\frac{x + 3}{4})+C$
(d) None of the above

Show Answer

Ans : (c) sin^-1 $(\frac{x + 3}{4})+C$

Q.29: If the area between x = y² and x = 4 is divided into two equal parts by the line x = a, then the value of a is
(a) (4)^1/3
(b) (4)^4/3
(c) (4)^2/3
(d) None of these

Show Answer

Ans : (c) (4)^2/3

Q.30: Area of the region bounded by the curve y = cos x between x = 0 and x = $\pi$ is
(a) 2 sq units
(b) 4 sq units
(c) 3 sq units
(d) 1 sq unit

Show Answer

Ans : (a) 2 sq units

Q.31: Area (in sq units) lying between the curves y² = 4x and y = 2x is
(a) $\frac23$
(b) $\frac13$
(c) $\frac14$
(d) $\frac34$

Show Answer

Ans : (b) $\frac13$

Q.32: The area of the circle x² + y² = 16 exterior to the parabola y² = 6x is
(a) $\frac43(4\pi-\sqrt3)$ sq units
(b) $\frac43(4\pi+\sqrt3)$ sq units
(c) $\frac43(8\pi-\sqrt3)$ sq units
(d) $\frac43(8\pi+\sqrt3)$ sq units

Show Answer

Ans : (c) $\frac43(8\pi-\sqrt3)$ sq units

Q.33: The equation of the form $2\frac{d^2y}{dx^2}+(\frac{dy}{dx})^3=0$ is a\an
(a) cubic equation
(b) quadratic equation
(c) ordinary differential equation
(d) None of the above

Show Answer

Ans : (c) ordinary differential equation

Q.34: The equation y = mx + c, where m and c are parameters, represents family of
(a) straight lines
(b) circles
(c) parabola
(d) hyperbola

Show Answer

Ans : (a) straight lines

Q.35: The equation of a curve whose tangent at any point on it different from origin has slope $y +\frac yx$ , is
(a) y = ex
(b) $y = kx.e^x$
(c) y = kx
(d) $y = x \cdot e^{x^2}$

Show Answer

Ans : (b) $y = kx.e^x$

Q.36: A differential equation of the form $\frac{dy}{dx}$ =F(x, y) is said to be homogeneous, if F(x, y) is a homogeneous function of degree
(a) 0
(b) 1
(c) 2
(d) 3

Show Answer

Ans : (a) 0

Q.37: If two or more vectors are parallel to the same line then they are called
(a) collinear vectors
(b) coinitial vectors
(c) equal vectors
(d) zero vectors

Show Answer

Ans : (a) collinear vectors

Q.38: If four points A(3,2,1), B(4, x, 5), C (4,2,-2) and D (6, 5,-1) are coplanar, then the value of x is
(a) 2
(b) 3
(c) 5
(d) 0

Show Answer

Ans : (c) 5

Q.39: In $\triangle$ ABC (fig), which of the following is not true?

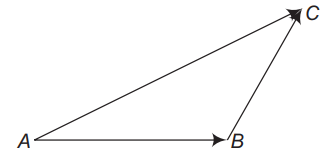
(a) AB + BC + CA = O
(b) AB + BC – AC = O
(c) AB + BC – CA = O
(d) AB – CB + CA = O

Show Answer

Ans : (c) AB + BC – CA = O

Q.40: If α,β,γ be the direction angles of a vector and cos α = $\frac{14}{15}$ , cosβ = $\frac13$ , then cos γ=……..K……. Here, K refers to
(a) ± $\frac{2}{15}$
(b) $\frac15$
(c) ± $\frac{1}{15}$
(d) None of these

Show Answer

Ans : (a) ± $\frac{2}{15}$

Q.41: The angle between the lines whose direction cosines are given by the equations 3l + m + 5n = 0 and 6mn – 2nl + 5lm=0, is
(a) cos^-1 $(\frac{1}{\sqrt6})$
(b) cos^-1 $(\frac{1}{3})$
(c) cos^-1 $(\frac{-1}{6})$
(d) cos^-1 $(\frac{-2}{3})$

Show Answer

Ans : (c) cos^-1 $(\frac{-1}{6})$

Q.42: The lines $\frac{x + 3}{-3}=\frac{y - 1}{1}=\frac{z-5}{5}$ and $\frac{x + 1}{-1}=\frac{y - 2}{2}=\frac{z-5}{5}$ are
(a) coplanar
(b) non-coplanar
(c) skew
(d) None of these

Show Answer

Ans : (a) coplanar

Q.43: The distance of the plane $r \cdot (\frac27 \hat i+\frac37 \hat j-\frac67 \hat k)=1$ from the origin is
(a) 1
(b) 7
(c) $\frac17$
(d) None of these

Show Answer

Ans : (a) 1

Q.44: The conditions $x \ge 0, y \ge 0$ are called
(a) restrictions only
(b) negative restrictions
(c) non-negative restrictions
(d) None of these

Show Answer

Ans : (c) non-negative restrictions

Q.45: The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy, where p, q > 0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
(a) p = q
(b) p = 2q
(c) q = 2p
(d) q = 3p

Show Answer

Ans : (d) q = 3p

Q.46: A diet is to contain atleast 80 units of vitamin A and 100 units of minerals. Two foods F₁ and F₂ are available. Food F₁ costs ₹ 4 per unit and food F₂ costs ₹ 6 per unit. One unit of food F₁ contains 3 units of vitamin A and 4 units of minerals. One unit of food F₂ contains 6 units of vitamin A and 3 units of minerals. Then, the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements, is
(a) ₹ 100
(b) ₹ 105
(c) ₹ 103
(d) ₹ 104

Show Answer

Ans : (d) ₹ 104

Q.47: One kind of cake requires 200g of flour and 25g of fat and another kind of cake requires 100g of flour and 50g of fat. Then, the maximum number of cakes which can be made from 5kg of flour and 1kg of fat assuming that there is no storage of the other ingredients used in making the cakes, is
(a) ₹ 20
(b) ₹ 10
(c) ₹ 30
(d) ₹ 40

Show Answer

Ans : (c) ₹ 30

Q.48: Let A and B be two events. If P(A)= 0.2, P(B) = 0.4 and P $(A \cup B) = 0.6$ , then P(A / B) is equal to
(a) 0.8
(b) 0.5
(c) 0.3
(d) 0

Show Answer

Ans : (d) 0

Q.49: Two dice are thrown. If it is known that the sum of numbers on the dice was less than 6, the probability of getting a sum 3, is
(a) $\frac {1}{18}$
(b) $\frac {5}{18}$
(c) $\frac {1}{5}$
(d) $\frac 25$

Show Answer

Ans : (c) $\frac {1}{5}$

Q.50: A description giving the values of the random variable along with the corresponding probabilities is called …K… of the random variable X. Here, K refers to
(a) conditional probability
(b) probability distribution
(c) mean
(d) None of the above

Show Answer

Ans : (b) probability distribution

Answer Key : CUET (UG) Mathematics Sample Paper

1. (d)	2. (a)	3. (a)	4. (b)	5. (d)	6. (b)	7. (c)	8. (c)	9. (d)	10. (d)
11. (b)	12. (b)	13. (c)	14. (d)	15. (b)	16. (b)	17. (a)	18. (c)	19. (a)	20. (c)
21. (d)	22. (a)	23. (a)	24. (a)	25. (b)	26. (b)	27. (c)	28. (c)	29. (c)	30. (a)
31. (b)	32. (c)	33. (c)	34. (a)	35. (b)	36. (a)	37. (a)	38. (c)	39. (c)	40. (a)
41. (c)	42. (a)	43. (a)	44. (c)	45. (d)	46. (d)	47. (c)	48. (d)	49. (c)	50. (b)

You may like : More CUET (UG) Sample Paper Archives

CUET (UG) Sample Paper : Mathematics

Related Posts

Leave a Comment