SSC CPO Quantitative Aptitude Questions with answers and Solutions. Maths MCQs Mock Test for free online practice of SI CAPF Exam.
Practice Set : Mathematics (Quantitative Aptitude)
Questions : 50
Medium : English
Level : SSC CPO SI Exam
All Type and topic MCQs – Solved by short tricks
Immediate display of Answer and Solution
New Practice of 50 Questions in every attempt
Results
#1. If out of 10 selected students for an examination, 3 were of 20 years age, 4 of 21 and 3 of 22 years, the average age of the group is :
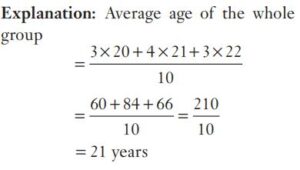
#2. The mean of 20 items is 55. If two items such as 45 and 30 are removed, the new mean of the remaining items is :
#3. If 28 men complete 
of a piece of work in a week, then the number of men, who must be engaged to get the remaining work completed in another week, is :
#4. The LCM of two multiples of 12 is 1056. If one of the number is 132, the other number is
#5. . Four years ago, the ratio of A’s age to B’s age was 11 : 14 and four years later their age will be in the ratio 13 : 16. The present age of A is :
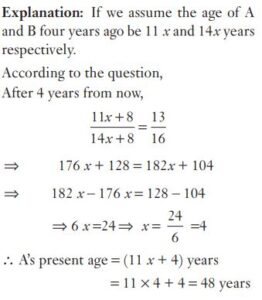
#6. A train passes a platform 90 metre long in 30 seconds and a man standing on the platform in 15 seconds. The speed of the train is :
#7. A train of length 120 m long, takes 6 seconds to pass a telegraph post, the speed of train is :
#8. Instead of multiplying a number by 0.72, a student multiplied it by 7.2. If his answer was 2592 more than the correct answer, then the original number was :
#9. A motor boat covers a certain distance downstream in a river in 3 hours. It covers the same distance upstream in 3 hours and a half. If the speed of water is 1.5 km/h, then the speed of the boat in still water is :
#10. 4 boys and 3 girls spent Rs.120 on the average, of which the boys spent Rs.150 on the average. Then the average amount spent by the girls is:
#11. A, B and C can do a piece of work in 30, 20 and 10 days respectively. A is assisted by B on one day and by C on the next day, alternately. How long would the work take to finish?
#12. The compound interest on a certain sum of money at a certain rate for 2 years is Rs 40.80 and the simple interest on the same sum is Rs 40 at the same rate and for the same time. The rate of interest is :
#13. 461+ 462 + 463 + 464 is divisible by
#14. In a test a student got 30% marks and failed by 25 marks. In the same test another student got 40% marks and secured 25 marks more than the essential minimum pass marks. The maximum marks for the test were
#15. A student was asked to multiply a given number by 
Instead, he divided the number by His answer was 225 more than the correct answer. The given number was :
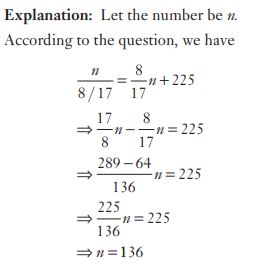
#16. On multiplying a number by 7, all the digits in the product appear as 3’s. The smallest such number is :
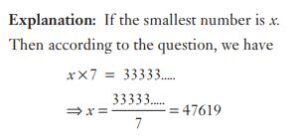
#17. 
is equal to
#18. If the price of a commodity is increased by 50%, by what fraction must its consumption be reduced so as to keep the same expenditure on its consumption?
#19. If the ratio of two numbers is 2 : 3 and their LCM is 54, then the sum of the two numbers is
Let the two numbers are 2x and 3x respectively.
According to question,
LCM = 54
x (3×2)=54
x = 9
Numbers = 2x = 2 × 9 = 18 and 3x = 3 × 9 = 27
Sum of the two numbers
= 18 27 = 45
#20. Ravi buys an article with a discount of 25% on its marked price. He makes a profit of 10% by selling it at Rs 660. The marked price of the article was :
#21. A farmer travelled a distance of 61 km in 9 hours. He travelled partly on foot at the rate of 4 kmph and partly on bicycle at the rate of 9 kmph. The distance travelled on foot is
#22. The average pocket money of 3 friends A, B, C is Rs. 80 in a particular month. If B spends double and C spends triple of what A spends during that month and if the average of their unspent pocket money is Rs. 60, then A spends (in Rs.)
#23. By selling a tape-recorder for Rs 1040 a man gains 4%. If he sells for Rs 950, then his loss will be :
#24. The ratio of two numbers is 3 : 8 and their difference is 115. The smaller of the two numbers is :
#25. The difference between the selling prices of an article at a profit of 15% and at a profit of 10% is Rs 10. The cost price of the article is
#26. if
=80, then P is equal to
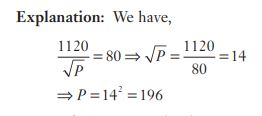
#27. the value of 25 – 5 [2 + 3 (2 – 2 (5 – 3) + 5) – 10] ÷ 4 is
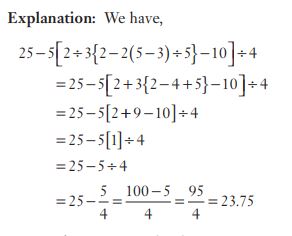
#28. If the selling price of 4 articles is equal to the cost price of 5 articles, the profit per cent is :
#29. A man bought an old type writer for Rs 1200 and spent Rs 200 on its repair. He sold it for Rs 1680. His profit per cent is :
#30. If the ratio of principal and the simple interest for 5 years is 10 : 3, then the rate of interest is :
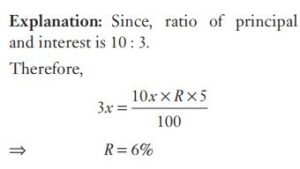
#31. Arvind spends 75% of his income and saves the rest. His income is increased by 20% and he increases his expenditure by 10%. Then the increase in savings in percentage is
#32. A number is first decreased by 20%. The decreased number is then increased by 20%. The resulting number is less than the original number by 20. Then the original number is
#33. Find the sum of the first five terms of the following series.
+………+…….
#34. The simplification of 
up to three places of decimals yields
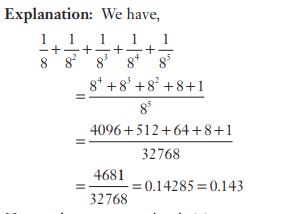
#35. The least number which when divided by 4, 6, 8, 12 and 16 leaves a remainder of 2 in each case is :
L.C.M. of 4, 6, 8, 12 and 16 = 48
Required number = 48 2 = 50
#36. When 75% of a number is added to 75, the result is the same number. Find the number.
#37. The average weight of the first 11 persons among 12 persons is 95 kg. The weight of 12th person is 33 kg more than the average weight of all the 12 persons. The weight of the 12th person is :
#38. Two numbers are in ratio 5 : 8. If their difference is 48, then the smaller number is :
#39. A boat goes 6 km an hour in still water, but takes thrice as much time in going the same distance against the current. The speed of the current (in km/hour) is :
#40. If a man walks 20 km at 5 km/hr, he will be late by 40 minutes. If he walks at 8 km/hr, how early from the fixed time will he reach?
#41. A vessel contains 20 litres of acid. 4 litres of acid is taken out of the vessel and replaced by the same quantity of water. The next 4 litres of the mixture are withdrawn and again the vessel is filled with the same quantity of acid left in the vessel with the quantity of acid initially in the vessel is :
#42. The simplified value of 
is
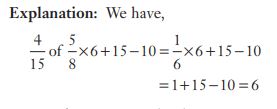
#43. Sunil completes a work in 4 days, whereas Dinesh completes the work in 6 days. Ramesh works 
times as fast as Sunil. The three together can complete the work in :
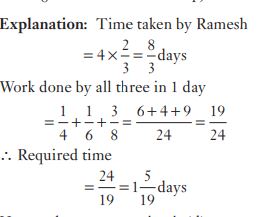
#44. The speed of two trains is in the ratio of 6 : 7. If the second train runs 364 km in 4 hours, then the speed of first train is ?
#45. At what rate percent per annum will the simple interest on a sum of money be 
of the amount in 10 years ?
#46. The smallest among![\sqrt[6]{12},\sqrt[3]4,\sqrt[4]5,\sqrt3](https://s0.wp.com/latex.php?latex=%5Csqrt%5B6%5D%7B12%7D%2C%5Csqrt%5B3%5D4%2C%5Csqrt%5B4%5D5%2C%5Csqrt3+&bg=ffffff&fg=000&s=0&c=20201002)
is
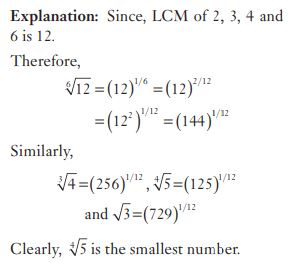
#47. The sum lent at 5% per annum (i.e., 365 days) simple interest that produces interest, of Rs 2.00 per day is :
#48. If a number is as much greater than 31 as it is less than 75, then the number is :
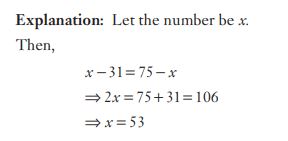
#49. Two numbers are less than a third number by 30% and 37% respectively. How much per cent is the second number less than the first?
#50. In one litre of a mixture of alcohol and water, water is 30%. The amount of alcohol that must be added to the mixture so that the part of water in the mixture becomes 15% is :
