Power Indices and Surds Maths Questions – Mock test for free online practice of SSC CGL, CHSL, CPO, GD, Bank competitive exams.
Quiz : Objective MCQs – Power Indices and Surds
All type Solved Questions from previous year paper
Results
#1. If 2 + x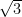 =
= then the simplest value of x is :
then the simplest value of x is :

#2. The smallest among![\sqrt[6]{12},\sqrt[3]4,\sqrt[4]5,\sqrt3](https://s0.wp.com/latex.php?latex=%5Csqrt%5B6%5D%7B12%7D%2C%5Csqrt%5B3%5D4%2C%5Csqrt%5B4%5D5%2C%5Csqrt3+&bg=ffffff&fg=000&s=0&c=20201002) is
is
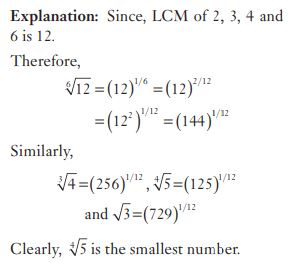
#3. The total number of prime factors in  is
is

#4. If the product of first 50 positive consecutive integers be divisible by  , where n is an integer, then the largest possible value of n is :
, where n is an integer, then the largest possible value of n is :

#5. If X =  , Y =
, Y =  , Z =
, Z = , then
, then
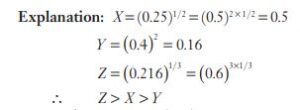
#6. The simplified value of  is
is

#7. 553 + 173 – 723 + 201960 is equal to
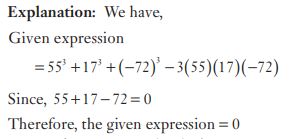
#8. Find the simplest value of  (given
(given
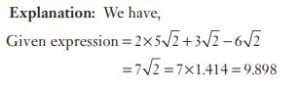
#9. The value of  is
is
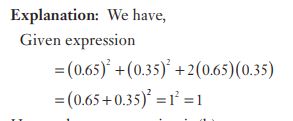
#10.  is equal to
is equal to
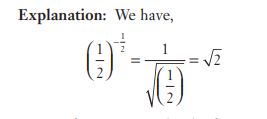
#11.  is equal to
is equal to

#12.  is equal to
is equal to

#13.  is equal to
is equal to

#14. Simplify: 

#15. By how much does  exceed
exceed  ?
?
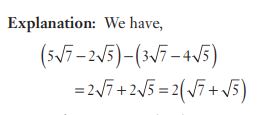
#16. The greatest number among  and
and  is
is
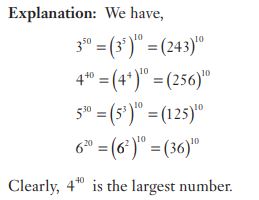
#17. If  , then the value of
, then the value of  up to three places of decimals is :
up to three places of decimals is :

#18. If  = 1.4142….. is given, then the value of
= 1.4142….. is given, then the value of  correct up to two decimal places is :
correct up to two decimal places is :
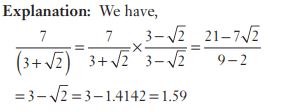
#19. The quotient when  is divided by
is divided by  is
is
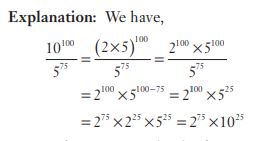
#20. If  then the value of x is :
then the value of x is :
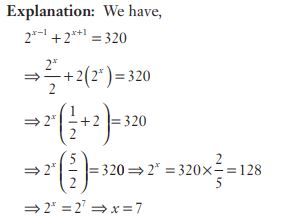
#21. If  , then the value of x is
, then the value of x is
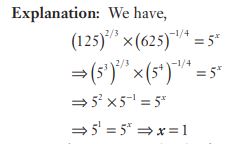
#22.  …….. is equal to
…….. is equal to

Press Finish / Submit to see the correct answer with solution and your result.