Geometry Objective Questions with Solution for SSC CGL, CHSL Competitive Exams. All type MCQs Mock Test for online practice.
Quiz : Geometry
Subject : Mathematics
Medium : English
Important questions with answer from previous year SSC papers
Solution with Short tricks
Press Finish / Submit button for the result and see the solution of all Geometry questions.
Results
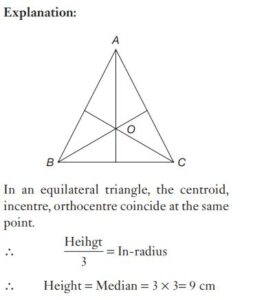
#1. The centroid of an equilateral triangle ABC is G and AB is 10 cm. The length of AG (in cm) is
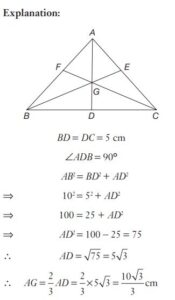
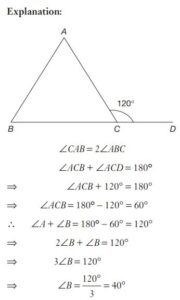
#2. The side BC of a triangle ABC is extended to D. If  and
and  , then the value of
, then the value of  is
is
#3. In a triangle, if three altitudes are equal, then the triangle is :
Explanation: Triangle will be equilateral.
Hence, the correct option is
#4. The in-radius of an equilateral triangle is of length 3 cm. Then the length of each of its medians is
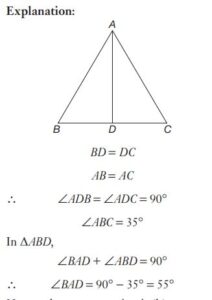
#5. ABC is an isosceles triangle such that AB = AC and AD is the median to the base BC with ∠ABC = 35°. Then ∠BAD is
#6. If angle bisector of a triangle bisects the opposite side, then what type of triangle is it?

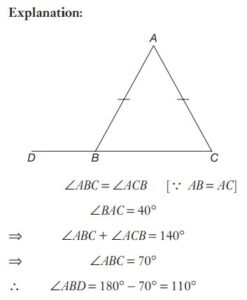
#7. In a triangle  Then the external angle at B is :
Then the external angle at B is :
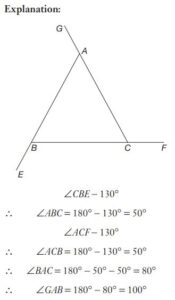
#8. ABC is a triangle and the sides AB, BC and CA are produced to E, F and G respectively. If  then the value of
then the value of  is
is
#9. In  , and
, and  , AD and AE are respectively the bisector of
, AD and AE are respectively the bisector of  and perpendicular on BC. The measure of
and perpendicular on BC. The measure of  is
is
#10. The side BC of a triangle ABC is produced to D. If  and
and  , then the measure of
, then the measure of 

#11. A man goes 24 m due west and then 10 m due north. Then the distance of him from the starting point is
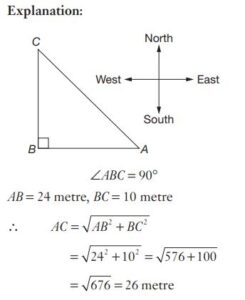
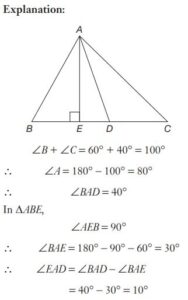
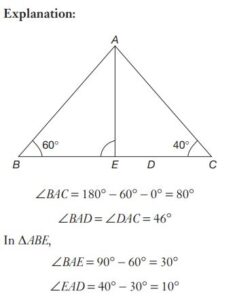
#12. In  is the bisector of
is the bisector of  and AE is drawn perpendicular on BC from A. Then the measure of
and AE is drawn perpendicular on BC from A. Then the measure of  is
is
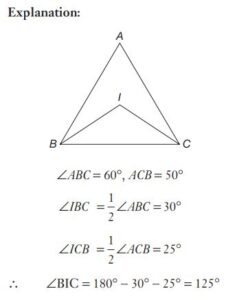
#13. I is the incentre of  and
and  . Then
. Then  is
is
#14. If the sides of a triangle are in the ratio  then the triangle is .
then the triangle is .

#15. In ∆ABC, ∠B = 90°, AB = 8 cm and BC = 15 cm, then sin C = ?

#16. If the sides of a right angled triangle are three consecutive integers, then the length of the smallest side is

#17. In a ∆ABC, D and E are two points on AB and AC respectively such that DE || BC, DE bisects the ∆ABC in two equal areas. Then the ratio of DB : AB is

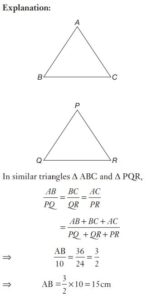
#18. The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then AB is
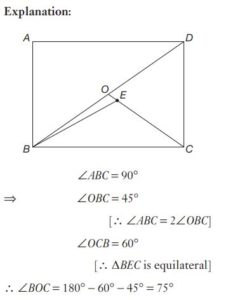
#19. Inside a square ABCD, ∆ BEC is an equilateral triangle. If CE and BD intersect at O, then ∠BOC is equal to
#20. The measure of each interior angle of a regular polygon with 8 sides is

#21. The sum of interior angles of a regular polygon is 1440° The number of sides of the polygon is

#22. The sum of all internal angles of a regular polygon whose one external angle is 20° is

#23. The number of sides in two regular polygons are in the ratio 5 : 4 and the difference between each interior angle of the polygons is 6°. Then the number of sides is :
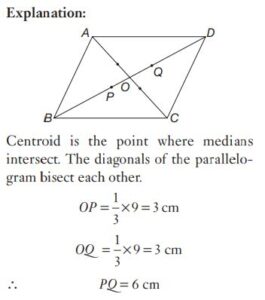
#24. The length of the diagonal BD of the parallelogram ABCD is 18 cm. If P and Q are the centroid of the ∆ABC and ∆ADC respectively then the length of the line segment PQ is :
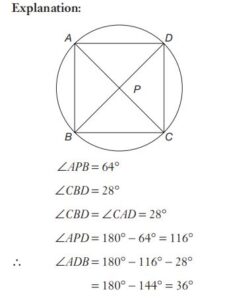
#25. The point of intersection of the diagonals AC and BD of the cyclic quadrilateral ABCD is P. If  and
and  . The measure of
. The measure of  is
is
#26. AB is a diameter of a circle having centre at O. PQ is a chord which does not intersect AB. Join AP and BQ. If  , then ABQP is a
, then ABQP is a
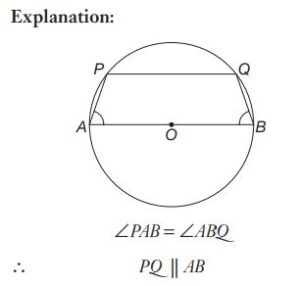
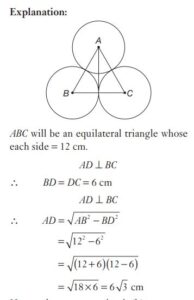
#27. Three circles of radius 6 cm each touch each other externally. Then the distance of the centre of one circle from the line joining the centres of other two circles is equal to
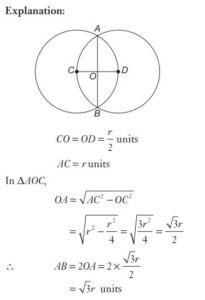
#28. Two circles having radii r units intersect each other in such a way that each of them passes through the centre of the other. Then the length of their common chord is
#29. The distance between two parallel chords of length 8 cm each in a circle of diameter 10 cm is

#30. Two circles with their centres at O and P and radii 8 cm and 4 cm respectively touch each other externally. The length of their common tangent is

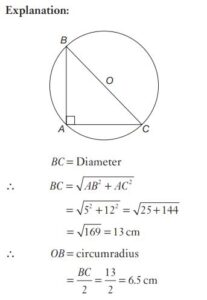
#31. If AB = 5 cm, AC = 12 cm and AB ⊥ AC, then the radius of the circumcircle of ∆ABC is
#32. The ratio of circumradius and radius of an equilateral triangle is

#33. A tree of hight ‘h’ metres is broken by a storm in such a way that it’s top touches the ground at a distance of ‘x’ metres from its root. Find the height at which the tree is broken. (Here 

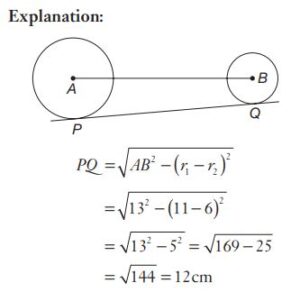
#34. A and B are centres of two circles of radii 11 cm and 6 cm respectively. PQ is a direct common tangent to the circles. If  = 13 cm, then the length of
= 13 cm, then the length of  will be
will be