SSC CGL Maths (Quantitative Aptitude) Questions with Solutions in Hindi. Mock Test of Previous Year Mathematics MCQs for free online practice.
विषय: गणित
स्तर: एसएससी सीजीएल
माध्यम: हिंदी
सेट में प्रश्न: 25 (प्रत्येक प्रयास में नया सेट)
नवीनतम पाठ्यक्रम के अनुसार सभी प्रकार के प्रश्न
शॉर्ट ट्रिक्स के साथ हल किए गए
Results
#1. अपनी सामान्य गति के  से चलकर एक व्यक्ति अपने कार्यालय अपने सामान्य समय से 20 मिनट देरी से पहुंचता है। कार्यालय पहुंचने में उसे सामान्यतः कितना समय लगता है?
से चलकर एक व्यक्ति अपने कार्यालय अपने सामान्य समय से 20 मिनट देरी से पहुंचता है। कार्यालय पहुंचने में उसे सामान्यतः कितना समय लगता है?

#2. एक परीक्षा में, एक छात्र को पास होने के लिए 36% अंक प्राप्त करने होंगे। 190 अंक प्राप्त करने वाला एक छात्र 35 अंकों से अनुत्तीर्ण हो गया। उस परीक्षा में कुल अंक हैं |

#3. एक नाव धारा के अनुकूल एक निश्चित दूरी तय करने में धारा के प्रतिकूल की अपेक्षा आधा समय लेती है। स्थिर जल में नाव की गति और धारा की गति का अनुपात है:

#4. एक व्यापारी अपने माल पर लागत मूल्य से 20% अधिक मूल्य अंकित करता है। वह अपने ग्राहकों को अंकित मूल्य पर 8% की छूट देता है। उसका लाभ प्रतिशत ज्ञात कीजिए |

#5. यदि पेट्रोल की कीमत 20% बढ़ा दी जाए, तो एक कार मालिक को अपनी खपत कितने प्रतिशत तक कम करनी होगी ताकि पेट्रोल पर उसका खर्च न बढ़े|

#6. एक कक्षा में 30 लड़के हैं और उनकी औसत आयु 17 वर्ष है। जब 18 वर्ष की आयु का एक लड़का कक्षा छोड़ देता है और दूसरा शामिल हो जाता है, तो औसत आयु 16.9 वर्ष हो जाती है। नए लड़के की आयु है|

#7.  किसके बराबर है ?
किसके बराबर है ?

#8. दिया गया है कि 12 + 22 + 32 + … + 202 = 2870. तो (22 + 42 + 62 + … + 402 ) का मान है:
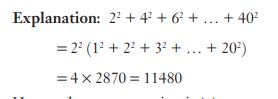
#9. साधारण ब्याज की किसी दर पर A ने B को 2 वर्ष के लिए 6000 रुपये तथा C को 4 वर्ष के लिए 1500 रुपये उधार दिए तथा दोनों से मिलाकर 900 रुपये ब्याज के रूप में प्राप्त किए। प्रति वर्ष ब्याज की दर थी?

#10. निम्नलिखित श्रृंखला के पहले पाँच पदों का योग ज्ञात कीजिए। +………+…….
+………+…….

#11. यदि 13 + 23 + … + 103 = 3025, तो 4 + 32 + 108 + … + 4000 बराबर है
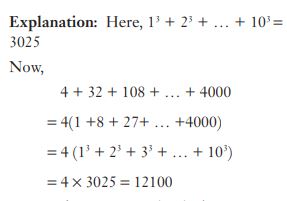
#12. एक किसान ने 9 घंटे में 61 किमी की दूरी तय की। उसने आंशिक रूप से 4 किमी प्रति घंटे की गति से पैदल और आंशिक रूप से 9 किमी प्रति घंटे की गति से साइकिल पर यात्रा की। पैदल तय की गई दूरी है?

#13. किसी निश्चित धनराशि पर 2 वर्षों के लिए एक निश्चित दर से चक्रवृद्धि ब्याज 40.80 रुपये है तथा उसी धनराशि पर उसी दर से तथा उसी समय के लिए साधारण ब्याज 40 रुपये है। ब्याज दर है:

#14. 30% एल्कोहल सामर्थ्य वाले मिश्रण को 50% एल्कोहल सामर्थ्य वाले मिश्रण के साथ किस अनुपात में मिलाया जाना चाहिए कि 45% एल्कोहल सामर्थ्य वाला मिश्रण प्राप्त हो?

#15. यदि प्रथम 50 क्रमागत धनात्मक पूर्णांकों का गुणनफल  से विभाज्य हो, जहाँ n एक पूर्णांक है, तो n का सबसे बड़ा संभावित मान क्या है?
से विभाज्य हो, जहाँ n एक पूर्णांक है, तो n का सबसे बड़ा संभावित मान क्या है?

#16. एक व्यापारी ने एक वस्तु को उसके लागत मूल्य के बराबर लाभ प्रतिशत पर 75 रुपये में बेचा। वस्तु का लागत मूल्य था|

#17. पाइप A एक टैंक को 4 घंटे में भर सकता है और पाइप B इसे 6 घंटे में भर सकता है। यदि उन्हें वैकल्पिक घंटों पर खोला जाता है और यदि पाइप A को पहले खोला जाता है, तो कितने घंटों में टैंक भर जाएगा?

#18. निम्नलिखित संख्याओं में सबसे बड़ी संख्या हैl


#19. एक आदमी ने एक पुराना टाइपराइटर 1200 रुपये में खरीदा और उसकी मरम्मत पर 200 रुपये खर्च किए। उसने उसे 1680 रुपये में बेच दिया। उसका लाभ प्रतिशत है |

#20.  का मान है?
का मान है?
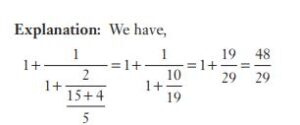
#21. यदि 10 वस्तुओं का क्रय मूल्य 9 वस्तुओं के विक्रय मूल्य के बराबर है, तो लाभ या हानि प्रतिशत होगा |

#22. यदि A और B का अनुपात 4 : 5 है तथा उनके वर्गों का अंतर 81 है, तो A का मान क्या है?

#23. रवि एक वस्तु को उसके अंकित मूल्य पर 25% की छूट पर खरीदता है। वह इसे 660 रुपये में बेचकर 10% का लाभ कमाता है। वस्तु का अंकित मूल्य था |

#24. एक वस्तु का मुद्रित मूल्य 900 रुपये है लेकिन खुदरा विक्रेता को 40% की छूट मिलती है। वह वस्तु को 900 रुपये में बेचता है। खुदरा विक्रेता का लाभ प्रतिशत है ?

#25. यदि दो धनात्मक संख्याओं का गुणनफल 1575 है तथा उनका अनुपात 7 : 9 है, तो सबसे बड़ी संख्या है ?
