SSC CHSL Quantitative Aptitude Questions with Solutions

SSC CHSL Quantitative Aptitude (Basic Arithmetic Skill) Questions with answers and Solutions for free online practice.

Mock Test : Maths (Quantitative Aptitude) MCQs
Exam : SSC CHSL
Medium : English
Questions : 25 ( New practice set in every attempt)
All questions are solved with short tricks
You can check the answer and solution of every question.

Results

#1. A 200 metre long train is running at a speed of 72 km/hr. How long will it take to cross 800 metre long bridge?

50 seconds

40 seconds

60 seconds

30 seconds

#2. The square of a natural number subtracted from its cube is 48. The number is

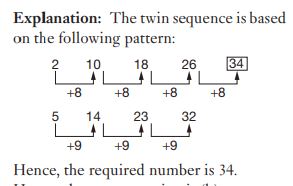
#3. The next number of the sequence 2, 5, 10, 14, 18, 23, 26, 32 … is

#4. A man, a woman and a boy can together complete a piece of work in 3 days. If a man alone can do it in 6 days and a boy alone in 18 days, how long will a woman alone take to complete the work?

9 days

21 days

24 days

27 days

#5. In a school 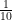$\frac{1}{10}$ of the boys are same in number as $\frac14$ of the girls and $\frac58$ of the girls are same in number as $\frac14$ of the boys. The ratio of the boys to girls in that school is :

2 : 1

5 : 2

4 : 3

3 : 2

#6. Of the 1000 inhabitants in a town 60% are males of whom 20% are literate. If from all the in-habitants, 25% are literate, then what percentage of the females of the town is literate?

27.5 %

32.5 %

37.5 %

22.5 %

#7. The HCF of two numbers is 96 and their LCM. is 1296. If one of the number is 864, the other is

132

135

140

144

#8. The value of ${3 +\frac{3}{3+\frac{1}{3+\frac{1}{3}}}}$ is

$\frac{40}{11}$

$\frac{43}{11}$

$\frac{46}{11}$

$\frac{41}{11}$

#9. A vessel contains 20 litres of acid. 4 litres of acid is taken out of the vessel and replaced by the same quantity of water. The next 4 litres of the mixture are withdrawn and again the vessel is filled with the same quantity of acid left in the vessel with the quantity of acid initially in the vessel is :

4 : 5

4 : 25

16 : 25

1 : 5

#10. If the average weight of 6 students is 50 kg; that of 2 students is 51 kg and that of 2 other students is 55 kg; then the average weight of all the students is :

61 kg

51.5 kg

52 kg

51.2 kg

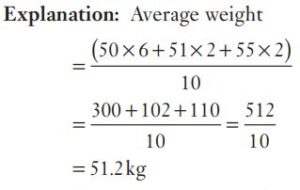
#11. Three years ago, the average age of a family of 5 members was 17 years. A baby having been born, the average age of the family is the same today. The present age of the baby (in year/s) is :

1.5

#12. If x is less than y by 25% then y exceeds x by

$33\frac{1}{3}$ %

25 %

75 %

$66\frac{2}{3}$%

#13. The odd term in the sequence 0, 7, 26, 63, 124, 217 is

217

#14. A and B can do a piece of work in 28 and 35 days respectively. They began to work together but A leaves after sometime and B completed the remaining work in 17 days. After how many days did A leave?

$14\frac25$ days

9 days

8 days

7$7\frac59$ days

#15. HCF of $\frac {2}{3} , \frac{4}{5} and \frac{6}{7}$ is

$ \frac{48}{105} $

$ \frac{2}{105} $

$ \frac{1}{105} $

$ \frac{24}{105} $

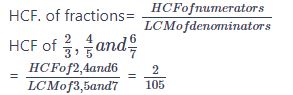
#16. On multiplying a number by 7, all the digits in the product appear as 3’s. The smallest such number is :

47649

47719

47619

48619

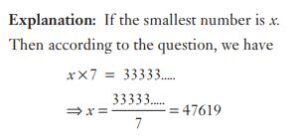
#17. If a boat goes 100 km downstream in 10 hours and 75 km upstream in 15 hours, then the speed of the stream is :

2 km/hour

2.5 km/hour

3 km/hour

3.5 km/hour

#18. Find the unit digit in the product
(4387)²⁴⁵ × (621)⁷²

#19. A and B can together finish a work in 30 days. They worked at it for 20 days and then B left. The remaining work was done by A alone in 20 more days A alone can finish the work in :

60 days

54 days

48 days

50 days

#20. A sum of money placed at compound interest doubles itself in 4 years. In how many years will it amount to four times itself ?

12 years

13 years

8 years

16 years

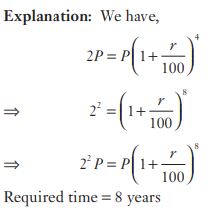
#21. A sum of Rs 1600 gives a simple interest of Rs 252 in 2 years and 3 months. The rate of interest per annum is :

$5\frac12$ %

8 %

7 %

6 %

#22. 84 Maths books, 90 Physics books and 120 Chemistry books have to be stacked topic wise. How many books will be there in each stack so that each stack will have the same height too ?

As the height of each stack is same, the required number of books in each stack
HCF of 84, 90 and 120
84 = 2 × 2 × 3 × 7, 90 = 2 × 3 × 3 × 5, 120 = 2 × 2 × 2 × 3 × 5
HCF = 2 × 3 = 6

#23. $\dfrac{(2.3)^3+0.027}{(2.3)^2-0.69+0.09}$ is equal to

2.6

2.00

2.33

2.80

#24. Three men can complete a piece of work in 6 days. Two days after they started the work, 3 more men joined them. How many days will they take to complete the remaining work?

1 days

2 days

3 days

4 days

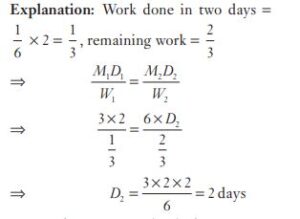
#25. The least number, which is to be added to the greatest number of 4 digits so that the sum may be divisible by 345 is :

FINISH