Trigonometry Questions for Competitive Exams

Trigonometry Questions with solution for Competitive Exams. Previous year Exam Question with official answer and detail explanation with short tricks. The Questions are as per SSC CGL and CHSL Exam Syllabus and Pattern. The below 1-18 questions are from the all shifts of SSC CHSL Exam.

Trigonometry Questions with Solution

Q.1: If (sin A – cos A) = 0 , then what is the value of cot A ?
(A) $\frac{\pi}{6}$
(B) 0
(C) 1
(D) $\frac{\pi}{4}$

Answer

Ans : (C) 1
(sin A – cos A) = 0
sin A = cos A
$\frac{cos A}{sin A} = 1$
cot A = 1

Q.2: If $cosec\theta=\frac{41}{9}$ and $\theta$ is an acute angle, then the value of $5 tan\theta$ will be:
(A) $\frac 98$
(B) $\frac {11}{8}$
(C) $\frac {13}{4}$
(D) $\frac 78$

Answer

Ans : (A) $\frac 98$
$cosec\theta=\frac{41}{9}$
$sin\theta=\frac{9}{41}$
पाइथागोरस प्रमेय से
BC² = 41²– 9²
$BC =\sqrt{1600} = 40$
ATQ $5 tan\theta = 5\times \frac{9}{40}$
$=\frac98$

Q.3: Solve the following equation and find the value of $\theta$ .
$3 cot\theta + tan \theta -2\sqrt3 = 0,0 <\theta < 90^o$
(A) 60^o
(B) 30^o
(C) 15^o
(D) 45^o

Answer

Ans : (A) 60^o
$3 cot\theta + tan \theta -2\sqrt3 = 0$
Put $\theta = 60$ its satisfy
3 x cot60 + tan60 -2 $\sqrt{3}$
$3\times\frac{1}{\sqrt3} +\sqrt3 - 2\sqrt3$
$\frac{3}{\sqrt3} +\sqrt3 - 2\sqrt3$
$\frac{6}{\sqrt3} -2\sqrt3$
$\frac {6-6}{\sqrt3} = \frac{0}{\sqrt3} = 0$
so $\theta = 60$

Q.4: In $\triangle ABC$ , $\angle A = 90^0$ , AB = 20cm and BC = 29cm. What is the value of (sinB -cotC) ?
(A) $\frac{189}{580}$
(B) $-\frac {9}{29}$
(C) $\frac{9}{29}$
(D) $-\frac{189}{580}$

Answer

Ans : (D) $-\frac{189}{580}$

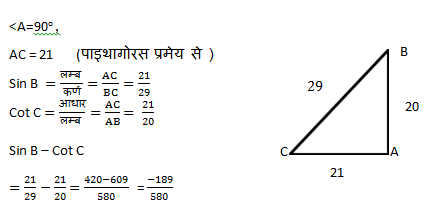
Trigonometry Questions for Competitive Exams

Q.5: If tanx = cot(48^o + 2x), and 0^o <x <90^o , then what is the value of x ?
(A) 14^o
(B 12^o
(C) 21^o
(D) 16^o

Answer

Ans : (A) 14^o
tan x = cot (48 + 2x)
tanx = tan (90 – (48 + 2x)
x = 90 -(48 + 2x)
x = 90 – 48 – 2x
3x = 42
x = 14

Q.6: If $7 sin^2\theta + 3cos^2\theta = 4,0^o <\theta <90^o$ , then the value of $\theta$ will be:
(A) 45^o
(B) 30^o
(C) 60^o
(D) 75^o

Answer

Ans : (B) 30^o
$7 sin^2\theta + 3cos^2\theta = 4$
$4 sin^2\theta + 3sin^2\theta +3cos^2\theta= 4$
$4 sin^2\theta + 3(sin^2 \theta + cos^2\theta)= 4$
$4sin^2\theta + 3\times1 = 4$
$4sin^2\theta = 4 - 3 = 1$
$sin^2\theta =\frac 14$
$sin\theta =\frac 12$
$\theta = 30^o$

Q.7: Find the value of $\theta$ , If sec² $sec^2\theta +(1 -\sqrt3)tan\theta -(1 +\sqrt3)=0$ , where $\theta$ is an acute angle.
(A) 30^o
(B) 15^o
(C) 60^o
(D) 45^o

Answer

Ans : (C) 60^o
$sec^2\theta +(1 -\sqrt3) tan\theta -(1 +\sqrt3) =0$
put $\theta = 60^o$ (By option)
$sec^2(60) + (1 -\sqrt3) tan 60 - (1 +\sqrt3)$
$4 +(1 - \sqrt3) \sqrt3 - (1 + \sqrt3)$
$4 +\sqrt3 - 3 - 1 -\sqrt3$
4 – 4 = 0
So $\theta = 60$

Q.8: If $cos\theta =\frac{7}{3\sqrt6}$ and $\theta$ is an acute angle, then the value of $27 sin^2\theta -\frac 32$ is:
(A) 15
(B) 12
(C) 1
(D) 9

Answer

Ans : (C) 1

Q.9: In a triangle ABC , right-angled at C, if sec A $=\frac{13}{5}$ , then find the value of $\frac{1+ sinA}{cosB}$ .
(A) $\frac{18}{5}$
(B) 5
(C) $\frac32$
(D) $\frac{25}{12}$

Answer

Ans : (D) $\frac{25}{12}$

Q.10: If $sin\theta + cosec \theta = 7$ , then what is the value of $sin^3\theta + cosec^3\theta$ ?
(A) 322
(B) 382
(C) 367
(D) 350

Answer

Ans : (A) 322
$sin\theta + cosec \theta = 7$
$(sin\theta + cosec \theta)^3 = 7^3$
$sin^3\theta + cosec^3 \theta +3sin\theta cosec\theta\times7 = 343$
$sin^3\theta + cosec^3 \theta +3\times7 = 343$ [ $Sin\theta\times Cosec\theta = 1$ ]
$sin^3\theta + cosec^3\theta = 343 - 21 = 322$
Trigonometry Questions for Competitive Exams

Q.11: If 3 cot A = 4 tan A , and A is an acute angle, then what will be the value of Sec A ?
(A) $\frac{\sqrt7}{2}$
(B) $\frac{1}{\sqrt3}$
(C) $\frac12$
(D) $\frac{\sqrt21}{3}$

Answer

Ans : (A) $\frac{\sqrt7}{2}$

Q.12: What is the value of $\frac{cos^220^o + cos^270^o}{sin^290^o} -tan^245^o$ ?
(A) -1
(B) 0
(C) -2
(D) 1

Answer

Ans : (B) 0
$\frac{cos^220^o + cos^270^o}{sin^290^o} -tan^245^o$
$\frac{1}{1} -1$ [Cos²20 + Cos²70 = 1, tan 45 = 1]
= 0

Q.13: If $\sqrt{13} Sin \theta = 2$ , then the value of $\frac{3tan\theta +\sqrt{13}Sin\theta}{\sqrt{13}Cos \theta-3 tan \theta}$ is:
(A) 5
(B) $\frac 12$
(C) 3
(D) 4

Answer

Ans : (D) 4

Q.14: In a right-angled triangle ABC right angled at C, Sin A = Sin B. What is the value of Cos A ?
(A) 1
(B) $\frac{\sqrt3}{2}$
(C) $\frac 12$
(D) $\frac{1}{\sqrt2}$

Answer

Ans : (D) $\frac{1}{\sqrt2}$
Sin A = Sin B
A = B = 45 Satisfy
Cos A = Cos 45
= $\frac{1}{\sqrt2}$

Q.15: If $5 Cos \theta = 4 Sin \theta , 0^o \leq \theta \leq 90^o$ , then what will be the value of $Sec \theta$ ?
(A) $\frac{\sqrt{41}}{4}$
(B) $\frac{\sqrt{41}}{16}$
(C) $\frac{\sqrt{41}}{5}$
(D) $\frac35$

Answer

Ans : (A) $\frac{\sqrt{41}}{4}$

Q.16: The value of $\frac{Cos 8^o Cos 24^o Cos 60^o Cos 66^o Cos 82^o}{Sin 82^o Sin 66^o Sin 60^o Sin 8^o Sin 24^o}$ is:
(A) $\frac{1}{\sqrt2}$
(B) $\frac{1}{\sqrt3}$
(C) 1
(D) 0

Answer

Ans : (B) $\frac{1}{\sqrt3}$
Cos 8^o Cos 82^o = 1
Cos 24^o Cos 60^o = 1
Sin 82^o Sin 8^o = 1
Sin 66^o Sin 24^o = 1
so $\frac{Cos 66^o}{Sin 60^o}$
$Cot 60=\frac{1}{\sqrt3}$

Q.17: If Sin B = $\frac{9}{41}$ , then what is the value of Cot B, where 0^o <B<90^o ?
(A) $\frac{9}{41}$
(B) $\frac{41}{9}$
(C) $\frac{9}{40}$
(D) $\frac{40}{9}$

Answer

Ans : (D) $\frac{40}{9}$

Q.18: If $tan\theta =\frac43$ , then the value of $\frac{9 Sin\theta + 12 Cos \theta}{27 Cos\theta -20sin \theta}$ will be equal to:
(A) 36
(B) 100
(C) 18
(D) 72